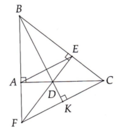
cho tam giác ABC. kẻ phân giác trong BD, CK. từ A kẻ đường thẳng vuông góc với CK tại M, từ A, C kẻ các đường thẳng vuông góc với BD tại N và L tương ứng, MN cắt AC tại E, BF cắt CL tại E
a, chứng minh MN//BC
b, chứng minh LF//AB và LF đi qua trung điểm BC
c, chứng minh DE//BC