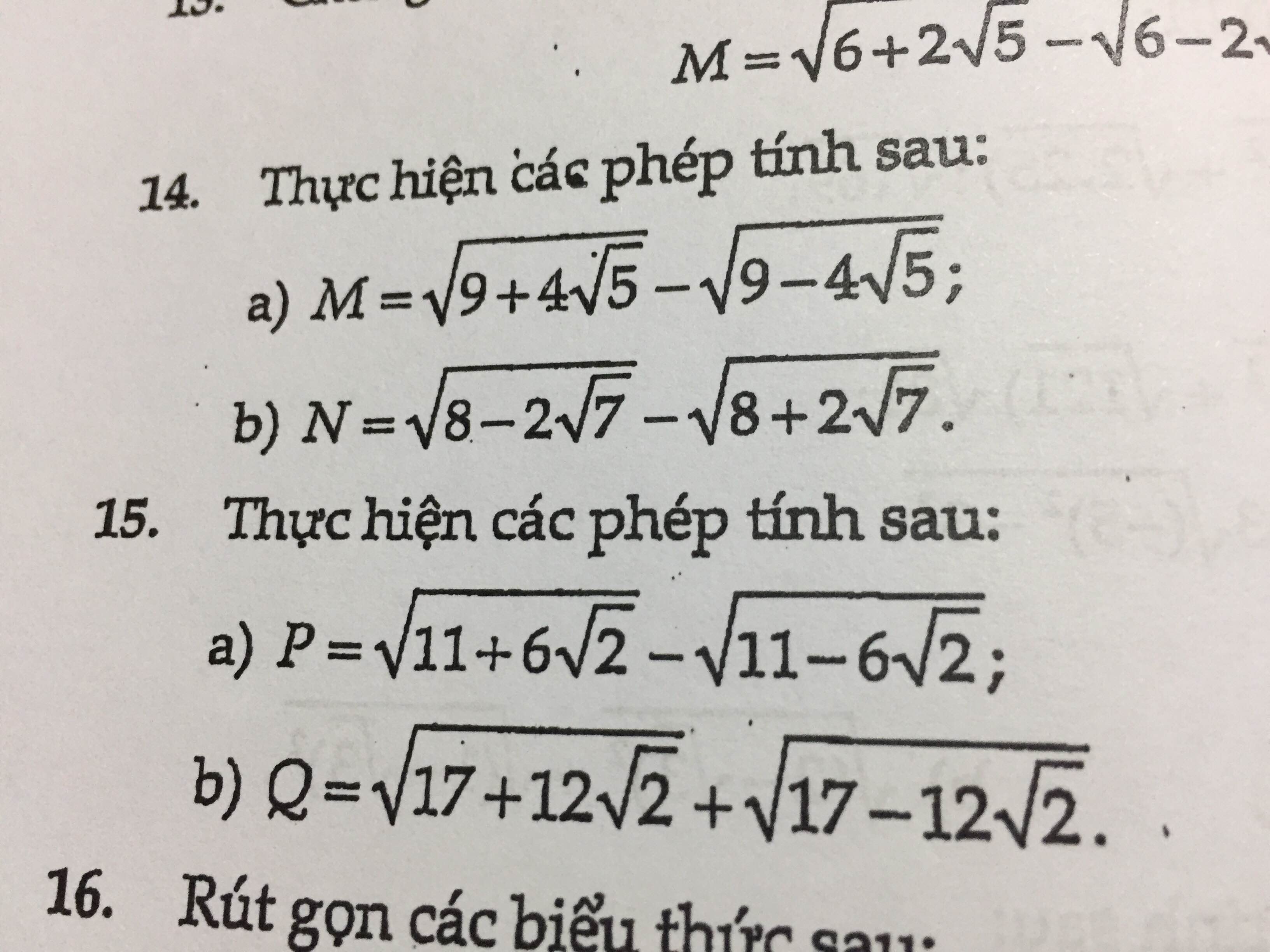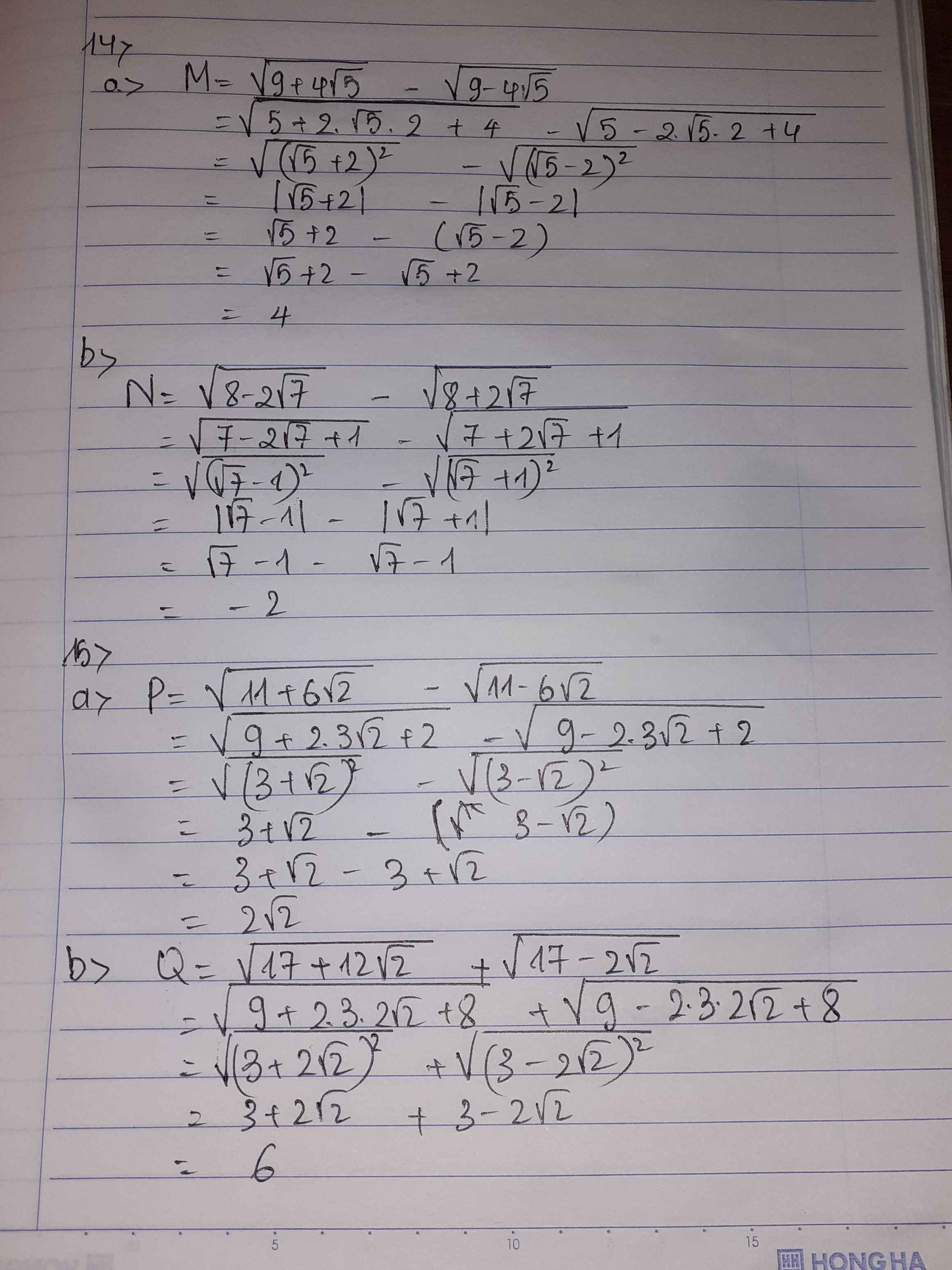giải thích hộ mk bài tỉ lệ nghịch cho dễ hiểu với (thanks)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Các bước giải bài toán tỉ lệ thuận, tỉ lệ nghịch
- Bước 1. Tóm tắt bài toán
- Bước 2. Phân tích bài toán, nhận dạng toán tỉ lệ thuận hay tỉ lệ nghịch
- Bước 3. Áp dụng 1 trong các cách (Rút về đơn vị, Rút về tỉ số, có thể áp dụng công thức tam suất) để giải bài toán.
- Bước 4. Kết luận, đáp số
Tỉ lệ thuận thì nhân
Tỉ lệ nghịch thì chia
Ví dụ 1: Tổ 4 lớp 5A có 15 em trồng được 90 cây. Hỏi cả lớp 45 em trồng được bao nhiêu cây? Biết số cây mỗi em trồng được bằng nhau ?
Tóm tắt:
15 em – 90 cây
45 em - a? cây
Bài giải:
1 em trồng được số cây là:
90 : 15 = 6 (cây)
45 em trông được số cây là:
6 x 45 = 270 (cây)
Đáp số: 270 cây
mình chỉ giải thích như mình hiểu:
Tỉ lệ nghịch là đối nhau,nên khi cái này tăng thì cái kia giảm,và tăng giảm cho tích luôn =nhau.Ví dụ dễ nhất là cùng 1 quãng đường ,nếu thời gian càng tăng thì vận tốc càng giảm(nghĩ nhé,cậu đi bộ từ nhà đến trường,vận tốc đi bộ và thời gian tỉ lệ nghịch với nhau nếu đi nhanh thì mất ít thời gian(đi chậm)thì ngược lại.
Tỉ lệ thuận là cùng chiều khi tăng hay giảm thì thì cái kia cũng vậy,ví dụ dễ nhất là điểm số(điểm kiểm tra và điểm trung bình có tỉ lệ thuận nếu kiểm tra càng cao thì trung bình càng cao
dễ hiểu mà

14a) \(M=\sqrt{9+4\sqrt{5}}-\sqrt{9-4\sqrt{5}}\)
\(=\sqrt{\left(\sqrt{5}\right)^2+2.\sqrt{2}.2+2^2}-\sqrt{\left(\sqrt{5}\right)^2-2.\sqrt{2}.2+2^2}\)
\(=\sqrt{\left(\sqrt{5}+2\right)^2}-\sqrt{\left(\sqrt{5}-2\right)^2}=\left|\sqrt{5}+2\right|-\left|\sqrt{5}-2\right|\)
\(=\sqrt{5}+2-\sqrt{5}+2=4\)
b) \(N=\sqrt{8-2\sqrt{7}}-\sqrt{8+2\sqrt{7}}\)
\(=\sqrt{\left(\sqrt{7}\right)^2-2.\sqrt{7}.1+1^2}-\sqrt{\left(\sqrt{7}\right)^2+2.\sqrt{7}.1+1^2}\)
\(=\sqrt{\left(\sqrt{7}-1\right)^2}-\sqrt{\left(\sqrt{7}+1\right)^2}=\left|\sqrt{7}-1\right|-\left|\sqrt{7}+1\right|\)
\(=\sqrt{7}-1-\sqrt{7}-1=-2\)
15a) \(P=\sqrt{11+6\sqrt{2}}-\sqrt{11-6\sqrt{2}}\)
\(=\sqrt{3^2+2.3.\sqrt{2}+\left(\sqrt{2}\right)^2}-\sqrt{3^2-2.3.\sqrt{2}+\left(\sqrt{2}\right)^2}\)
\(=\sqrt{\left(3+\sqrt{2}\right)^2}-\sqrt{\left(3-\sqrt{2}\right)^2}=\left|3+\sqrt{2}\right|-\left|3-\sqrt{2}\right|\)
\(=3+\sqrt{2}-3+\sqrt{2}=2\sqrt{2}\)
b) \(Q=\sqrt{17+12\sqrt{2}}+\sqrt{17-12\sqrt{2}}\)
\(=\sqrt{3^2+2.3.2\sqrt{2}+\left(2\sqrt{2}\right)^2}+\sqrt{3^2-2.3.2\sqrt{2}+\left(2\sqrt{2}\right)^2}\)
\(=\sqrt{\left(3+2\sqrt{2}\right)^2}+\sqrt{\left(3-2\sqrt{2}\right)^2}=\left|3+2\sqrt{2}\right|+\left|3-2\sqrt{2}\right|\)
\(=3+2\sqrt{2}+3-2\sqrt{2}=6\)

Xem thêm tại: https://loigiaihay.com/ly-thuyet-dai-luong-ti-le-nghich-c42a4616.html#ixzz7EB2Exm8D

Định nghĩa
Nếu một đại lượng y liên hệ với một đại lượng x theo công thức: y = k.x (k hằng số khác 0) thì ta nói y tỉ lệ thuận với x theo hệ số tỉ lệ k.
Tính chất
Nếu hai đại lượng x và y tỉ lệ thuận:
Tỉ số hai giá trị tương ứng của chúng luôn không đổi.
Tỉ số hai giá trị bất kỳ của đại lượng này bằng Tỉ số hai giá trị tương ứng của đại lượng kia.
Tỉ lệ thuận là mối tương quan giữa hai đại lượng x và y mà trong đó sự gia tăng về giá trị của đại lượng x bao nhiêu lần luôn kéo theo sự gia tăng tương ứng về giá trị của đại lượng y bấy nhiêu lần, và ngược lại. Trong toán học thì đại lượng tỉ lệ thuận trái ngược với đại lượng tỉ lệ nghịch.
Định nghĩa
Nếu một đại lượng y liên hệ với một đại lượng x theo công thức: y = k.x (k hằng số khác 0) thì ta nói y tỉ lệ thuận với x theo hệ số tỉ lệ k.
Tính chất tỉ lệ thuận
Nếu đại lượng x tỉ lệ thuận với đại lượng y thì có những tính chất sau
- Tỉ số hai giá trị tương ứng của chúng luôn không đổi.
- Tỉ số hai giá trị bất kỳ của đại lượng này bằng tỉ số hai giá trị tương ứng của đại

xy=-12
=>y=-12/x
y=3z
=>-12/x=3z
=>3xz=-12
=>xz=-4
Vậy: x và z tỉ lệ nghịch theo hệ số tỉ lệ k=-4