Cho S=\(\frac{2}{3-\sqrt{x}}\)với x> hoặc =0, x #4. Tìm x để S= 1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
14 tháng 8 2016
Áp dụng BĐT Cô si ta có:
\(x+y\ge2\sqrt{xy}=2\cdot\frac{1}{\sqrt{z}};y+z\ge2\sqrt{yz}=2\cdot\frac{1}{\sqrt{x}};z+x\ge2\sqrt{xz}=2\cdot\frac{1}{\sqrt{y}}.\)( vì xyz=1)
=> P\(\ge\)\(\frac{2x\sqrt{x}}{y\sqrt{y}+2z\sqrt{z}}\)+ \(\frac{2y\sqrt{y}}{z\sqrt{z}+2x\sqrt{x}}+\frac{2z\sqrt{z}}{x\sqrt{x}+2y\sqrt{y}}\)
Đặt \(\hept{\begin{cases}a=y\sqrt{y}+2z\sqrt{z}\\b=z\sqrt{z}+2x\sqrt{x}\\c=x\sqrt{x}+2y\sqrt{y}\end{cases}\left(a;b;c\ge0\right)}\)<=> \(\hept{\begin{cases}4a+b=2c+9z\sqrt{z}\\4b+c=2a+9x\sqrt{x}\\4c+a=2b+9y\sqrt{y}\end{cases}}\)
<=> \(\hept{\begin{cases}z\sqrt{z}=\frac{4a+b-2c}{9}\\x\sqrt{x}=\frac{4b+c-2a}{9}\\y\sqrt{y}=\frac{4c+a-2b}{9}\end{cases}}\)
Do đó:
P \(\ge\)\(\frac{2}{9}\cdot\left(\frac{4a+b-2c}{c}+\frac{4b+c-2a}{a}+\frac{4c+a-2b}{b}\right)\)
<=> P \(\ge\)\(\frac{2}{9}\left(4\left(\frac{a}{c}+\frac{b}{a}+\frac{c}{b}\right)+\left(\frac{b}{c}+\frac{c}{a}+\frac{a}{b}\right)-6\right)\)
<=> P \(\ge\frac{2}{9}\cdot\left(4\cdot3\cdot\sqrt[3]{\frac{a}{c}\cdot\frac{b}{a}\cdot\frac{c}{b}}+3\cdot\sqrt[3]{\frac{b}{c}\cdot\frac{c}{a}\cdot\frac{a}{b}}-6\right)\)( Áp dụng BĐT Cô si cho 3 số ko âm)
<=> P \(\ge\frac{2}{9}\left(12+3-6\right)=2\)( đpcm)
Dấu = khi x=y=z=1.
23 tháng 7 2020
\(B=\frac{2}{x^2-y^2}\cdot\sqrt{\frac{9\left(x^2+2xy+y^2\right)}{4}}=\frac{2}{\left(x-y\right)\left(x+y\right)}\cdot\sqrt{\frac{9\left(x+y\right)^2}{4}}\)
\(=\frac{2}{\left(x-y\right)\left(x+y\right)}\cdot\frac{\sqrt{9\left(x+y\right)^2}}{\sqrt{4}}=\frac{2}{\left(x-y\right)\left(x+y\right)}\cdot\frac{3\left(x+y\right)}{2}\)(vì x > -y <=> x + y > 0)
\(=\frac{3}{x-y}\)
\(C=\sqrt{\frac{2a}{3}}.\sqrt{\frac{3a}{8}}=\sqrt{\frac{2a}{3}\cdot\frac{3a}{8}}=\sqrt{\frac{6a^2}{24}}=\sqrt{\frac{a^2}{4}}=\frac{a}{2}\)(vì a > = 0)
\(D=\frac{1}{a-b}\cdot\sqrt{a^4\left(a-b\right)^2}=\frac{1}{a-b}\cdot a^2\left(a-b\right)=a^2\)(a > b > 0)
23 tháng 7 2020
câu cuối điều kiện là a>b
\(\frac{1}{a-b}\sqrt{a^4\left(a-b\right)^2}=\frac{a^2\left|a-b\right|}{a-b}=\frac{a^2\left(a-b\right)}{a-b}=a^2\) (vì a>b)
VT
3
10 tháng 10 2021
\(M=\frac{\sqrt{x}}{\sqrt{x}+1}\left(x\ge0\right)\)
Khi \(M=\sqrt{x}-2\)
\(\Rightarrow\frac{\sqrt{x}}{\sqrt{x}+1}=\sqrt{x}-2\)
\(\Leftrightarrow\sqrt{x}=\left(\sqrt{x}-2\right)\left(\sqrt{x}+1\right)\)
\(\Leftrightarrow\sqrt{x}=x+\sqrt{x}-2\sqrt{x}-2\)
\(\Leftrightarrow\sqrt{x}=x-\sqrt{x}-2\)
\(\Leftrightarrow x-\sqrt{x}-\sqrt{x}-2=0\)
\(\Leftrightarrow x-2\sqrt{x}+1-3=0\)
\(\Leftrightarrow\left(\sqrt{x}-1\right)^2=3\)
\(\Leftrightarrow\left(\sqrt{x}-1\right)^2=\left(\pm\sqrt{3}\right)^2\)
\(\Leftrightarrow\sqrt{x}-1=\pm\sqrt{3}\)
\(\Leftrightarrow\sqrt{x}=\pm\sqrt{3}+1\)
\(\Leftrightarrow\orbr{\begin{cases}x=\left(\sqrt{3}+1\right)^2\\x=\left(-\sqrt{3}+1\right)^2\end{cases}}\)
\(\Leftrightarrow\orbr{\begin{cases}x=3+2\sqrt{3}+1\\1-2\sqrt{3}+3\end{cases}}\)
\(\Leftrightarrow\orbr{\begin{cases}x=4+2\sqrt{3}\\x=4-2\sqrt{3}\end{cases}}\)
Vậy \(x\in\left\{4\pm2\sqrt{3}\right\}\)khi \(M=\sqrt{x}-2\)
NV
Nguyễn Việt Lâm
Giáo viên
4 tháng 8 2020
\(A=\frac{\left(x+4\right)-\sqrt{x}}{2\sqrt{x}}\ge\frac{2\sqrt{4x}-\sqrt{x}}{2\sqrt{x}}=\frac{3\sqrt{x}}{2\sqrt{x}}=\frac{3}{2}\)
\(A_{min}=\frac{3}{2}\) khi \(x=4\)
\(B=\frac{x+3+2\sqrt{x}}{\sqrt{x}}\ge\frac{2\sqrt{3x}+2\sqrt{x}}{\sqrt{x}}=2\sqrt{3}+2\)
\(B_{min}=2\sqrt{3}+2\) khi \(x=3\)
Xem lại đề câu C, với \(x>0\) thì \(C_{min}\) ko tồn tại
GJ
4 tháng 8 2020
Bạn ơi cho mình hỏi tại sao \(\frac{\left(x+4\right)-\sqrt{x}}{2\sqrt{x}}\)lại lớn hơn hoặc bằng \(\frac{2\sqrt{4x}-\sqrt{x}}{2\sqrt{x}}\)vậy ạ?
3 tháng 9 2016
a) \(\frac{x\sqrt{x}+y\sqrt{y}}{\sqrt{x}+\sqrt{y}}-\left(\sqrt{x}-\sqrt{y}\right)^2\)
\(=\frac{\left(\sqrt{x}+\sqrt{y}\right)\left(x-\sqrt{xy}+y\right)}{\sqrt{x}+\sqrt{y}}-\left(x-2\sqrt{xy}+y\right)\)
\(=x-\sqrt{xy}+y-x+2\sqrt{xy}-y=\sqrt{xy}\)
b) \(\sqrt{\frac{x-2\sqrt{x}+1}{x+2\sqrt{x}+1}}=\sqrt{\frac{\left(\sqrt{x}-1\right)^2}{\left(\sqrt{x}+1\right)^2}}=\frac{\left|\sqrt{x}-1\right|}{\sqrt{x}+1}\)
c) \(4x-\sqrt{8}+\frac{\sqrt{x^3+2x^2}}{\sqrt{x+2}}=4x-\sqrt{8}+\frac{\sqrt{x^2\left(x+2\right)}}{x+2}=4x-\sqrt{8}+x=5x-\sqrt{8}\)
NV
Nguyễn Việt Lâm
Giáo viên
10 tháng 2 2020
b/ Ko biết yêu cầu
4/ \(E=\frac{x^2}{3}+\frac{x^2}{3}+\frac{x^2}{3}+\frac{1}{x^3}+\frac{1}{x^3}\ge5\sqrt[5]{\frac{x^6}{27x^6}}=\frac{5}{\sqrt[5]{27}}\)
Dấu "=" xảy ra khi \(\frac{x^2}{3}=\frac{1}{x^3}\Leftrightarrow x=\sqrt[5]{3}\)
\(F=x+\frac{1}{x^2}=\frac{x}{2}+\frac{x}{2}+\frac{1}{x^2}\ge3\sqrt[3]{\frac{x^2}{4x^2}}=\frac{3}{\sqrt[3]{4}}\)
Dấu "=" xảy ra khi \(\frac{x}{2}=\frac{1}{x^2}\Rightarrow x=\sqrt[3]{2}\)
6/ \(Q=\frac{\left(x+1\right)^2+16}{2\left(x+1\right)}=\frac{x+1}{2}+\frac{8}{x+1}\ge2\sqrt{\frac{8\left(x+1\right)}{2\left(x+1\right)}}=4\)
Dấu "=" xảy ra khi \(\frac{x+1}{2}=\frac{8}{x+1}\Leftrightarrow x=3\)
NV
Nguyễn Việt Lâm
Giáo viên
10 tháng 2 2020
7/
\(R=\frac{\left(\sqrt{x}+3\right)^2+25}{\sqrt{x}+3}=\sqrt{x}+3+\frac{25}{\sqrt{x}+3}\ge2\sqrt{\frac{25\left(\sqrt{x}+3\right)}{\sqrt{x}+3}}=10\)
Dấu "=" xảy ra khi \(\sqrt{x}+3=\frac{25}{\sqrt{x}+3}\Leftrightarrow x=4\)
8/
\(S=x^2+\frac{2000}{x}=x^2+\frac{1000}{x}+\frac{1000}{x}\ge3\sqrt[3]{\frac{1000^2x^2}{x^2}}=300\)
Dấu "=" xảy ra khi \(x^2=\frac{1000}{x}\Leftrightarrow x=10\)
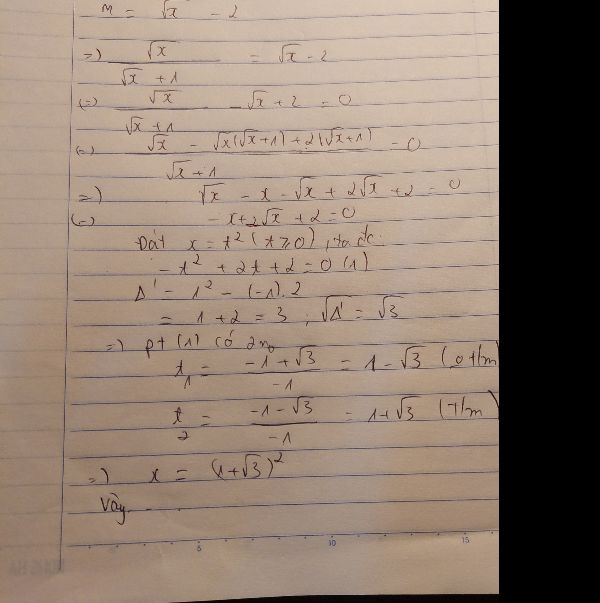
Để S = 1
\(\Rightarrow3-\sqrt{x}=2:1=2\)
\(\Rightarrow\sqrt{x}=3-2=1\)
\(\Rightarrow x=1\)
Để S = 1
\(\Rightarrow3-\sqrt{x}=2.1=2\)
\(\Rightarrow\sqrt{x}=3-2=1\)
\(\Rightarrow x=1\)