Cho hình bình hành ABCD, M là một điểm bất kì trên cạnh CD, AM cắt BD ở O. Chứng minh rằng SABO = SDMO+SEMC
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
KN
6 tháng 2 2020
Áp dụng định lý Thalès, ta có:
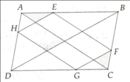
HE // BD \(\Rightarrow\frac{AH}{AD}=\frac{AE}{AB}\)(1)
EF // AC \(\Rightarrow\frac{AE}{AB}=\frac{FC}{BC}\)(2)
FG // BD \(\Rightarrow\frac{FC}{BC}=\frac{GC}{DC}\)(3)
Từ (1),(2),(3) suy ra \(\frac{AH}{AD}=\frac{GC}{DC}\Rightarrow AH.CD=AD.CG\left(đpcm\right)\)
VN
0
17 tháng 1 2017
Cho hình vuông ABCD, O là giao điểm hai đường chéo AC và BD. Qua O kẻ các đường thẳng lần lượt vuông góc với AB,BC,CD,DA tại E,G,F,H.Chứng minh:
a) Bà điểm E,O,F thẳng hàng và ba điểm G,O,H thẳng hàng
b) Tứ giác EGFH lầ hình vuông
PA
ABCD là hình bình hành, M thuộc CD. MA và BD cắt nhau ở O. Chứng minh:
a) SAOD=SOMB
b)SABO=SDMO+SBMC
0
23 tháng 10 2021
a: Xét ΔAOM và ΔCON có
\(\widehat{MAO}=\widehat{NCO}\)
OA=OC
\(\widehat{AOM}=\widehat{CON}\)
Do đó: ΔAOM=ΔCON
Suy ra: AM=CN
*SABO = SDMO+SBMC
mình có kết quả giống vơi Luyến nhé