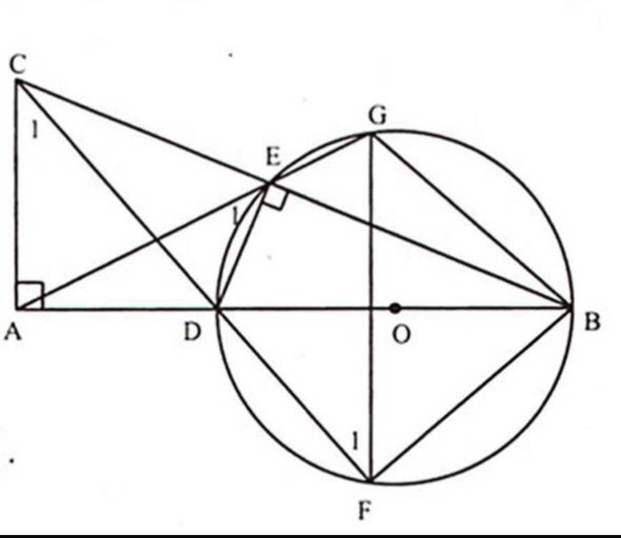
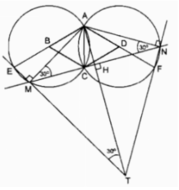
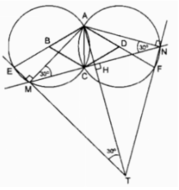
Cho tam giác ABC vuông tại A. Lấy điểm M tùy ý nằm giữa A và B. Dường tròn đường kính BM cắt BC tại điểm thứ hai là E. Các đường thẳng CM, AE lần lượt cắt đường tròn tại các điểm thứ hai là H, K.
a, CM: tứ giác AMEC nội tiếp
b, CM: góc ACM bằng góc KHM
c, CM: BH, EM, AC đồng quy
d, Giả sử AC<AB, hãy xác định vị trí của điểm M để tứ giác AHBC là hình thang cân.
GIÚP MÌNH VS MỌI NGƯỜI ƠI!!!




Ta có: góc BEM=90độ (góc nội tiếp chắn nửa đường tròn) => góc MEC=90độ
Xét tứ giác AMEC có: góc MEC + góc MAC= 90độ + 90độ = 180độ => AMEC nội tiếp
=> góc ACM = góc MEK (cùng chắn cung MA)
Mà HMKE nội tiếp đường tròn đường kính BM => góc KHM = góc MEK (cùng chắn cung MK)
=> góc ACM = góc KHM
Gọi P là giao điểm của BH và AC
Ta có: CH vuông góc BP (do góc CHB= góc MHB=90độ) , BA vuông góc AC và BA cắt HC tại M => M là trực tâm tam giác BPC
=> PM vuông góc BC
Mà ME vuông góc BC
=> P, M, E thẳng hàng
=> BH, ME, AC đồng qui tại P
Ta có: góc BEM=90độ (góc nội tiếp chắn nửa đường tròn) => góc MEC=90độ
Xét tứ giác AMEC có: góc MEC + góc MAC= 90độ + 90độ = 180độ => AMEC nội tiếp
=> góc ACM = góc MEK (cùng chắn cung MA)
Mà HMKE nội tiếp đường tròn đường kính BM => góc KHM = góc MEK (cùng chắn cung MK)
=> góc ACM = góc KHM
Gọi P là giao điểm của BH và AC
Ta có: CH vuông góc BP (do góc CHB= góc MHB=90độ) , BA vuông góc AC và BA cắt HC tại M => M là trực tâm tam giác BPC
=> PM vuông góc BC
Mà ME vuông góc BC
=> P, M, E thẳng hàng
=> BH, ME, AC đồng qui tại P