viết số tự nhiên có 5 chữ số lập nên từ 2 chữ số 0 và 1, mà trong đó chữ số 1 được có mặt 3 lần
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Viết các số tự nhiên có 5 chữ số lập nên từ hai chữ số 0 ; 1 mà trong đó chữ số 1 được có mặt ba lần


Giả sử số cần tìm là abcd
Ta thực hiện các bước sau:
Số cần tìm là số tự nhiên nên a ≠ 0 suy ra a = 1. Như vậy ta còn chữ số 1 và hai chữ số 0 để xếp vào 3 vị trí còn lại
Nếu xếp chữ số 0 vào vị trí b thì ta được số cần tìm là 1001 hoặc1010
Nếu xếp chữ số 1 vào vị trí b thì ta được số cần tìm là 1100Vậy ta có ba số cần tìm là 1001; 1010; 1100
Đáp án B

Chọn C
Ta có thể chia làm bốn trường hợp sau
TH1: Số 5 có mặt một lần, số 6 có mặt một lần.( Bao gồm các khả năng sau: mỗi số có mặt một lần hoặc một số 5, một số 6 hai số 3 hoặc một số 5, một số 6 hai số 4)
Số các số được tạo thành là: 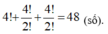
TH2: Số 5 có mặt một lần, số 6 không có mặt.
Số các số được tạo thành là: 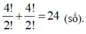
TH3: Số 6 có mặt một lần, số 5 không có mặt.
Số các số được tạo thành là: 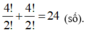
TH4: Số 5 và số 6 không có mặt.( Số 3 và số 4 mỗi số có mặt đúng hai lần)
Số các số được tạo thành là: 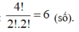
Vậy có thể lập được 102 số thỏa mãn đề bài.

TH1: số 2 đứng đầu:
Chọn 2 chữ số từ 6 chữ số còn lại và hoán vị: \(A_6^2=30\) cách
TH2: số 2 không đứng đầu:
Chọn số hàng trăm: có 5 cách (khác 0 và 2)
Chọn 1 chữ số còn lại: 5 cách, hoán vị nó với 2: có \(2!=2\) cách
\(\Rightarrow5.5.2=50\) cách
Tổng cộng: \(30+50=80\) số

Các số là:
2035;2053;2305;2350;2503;2530;3025;3052;3205;3250;3502;3520;5023;5032;5203;5230;5302;5320
2035+2053+2305+2350+2503+2530+3025+3052+3205+3250+3502+3520+5023+5032+5203+5230+5302+5320=44563

| Số chữ số \(3\)\(\left(\le2\right)\) | Số chữ số \(4\) \(\left(\le2\right)\) | Số chữ số \(5\)\(\left(\le1\right)\) | Số chữ số \(6\)\(\left(\le1\right)\) | Số số tự nhiên lập được |
| 0 | 2 | 1 | 1 | 12 |
| 1 | 1 | 1 | 1 | 24 |
| 1 | 2 | 1 | 0 | 12 |
| 1 | 2 | 0 | 1 | 12 |
| 2 | 0 | 1 | 1 | 12 |
| 2 | 1 | 0 | 1 | 12 |
| 2 | 1 | 1 | 0 | 12 |
| 2 | 2 | 0 | 0 | 6 |
Ta được 12.6+24+6=102 số thỏa mãn

Số chữ số tìm được là \(\dfrac{C^2_5\cdot5!}{3!}=200\)
Số số chia hết cho 3 là \(\dfrac{2\cdot5!}{3!}=40\)
\(\Rightarrow P=\dfrac{40}{200}=\dfrac{1}{5}\)
các số đó là
10101
11100
10011
11001
11010