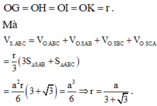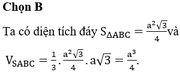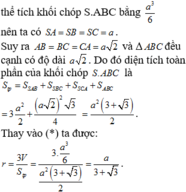Tính thể tích của một hình chóp tam giác đều, biết SA=5cm, SO=3cm
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
7 tháng 6 2019
a) Ta có: AC2 = AB2 + BC2 (Pytago) = 32 + 32 = 18(cm)
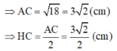
Lại có: SH2 = SC2 - HC2 (Pytago)
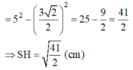
b) Gọi K là trung điểm của BC
Ta có: SK2 = SH2 + HK2 (Pytago)
13 tháng 8 2023
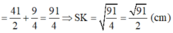
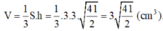
a: S.ABC là hình chóp đều
=>SA=SB=SC và AB=AC=BC
ΔSAB cân tại S có SM là trung tuyến
nên SM vuông góc AB
=>ΔSMA vuông tại M
\(MA=\sqrt{SA^2-SM^2}=2\left(cm\right)\)
=>BA=2*2=4cm=BC=AC
b: \(S_{Xq}=\dfrac{1}{2}\left(4+4+4\right)\cdot5=6\cdot5=30\left(cm^2\right)\)
c: \(S_{tp}=30+4^2\cdot\dfrac{\sqrt{3}}{4}=30+4\sqrt{3}\left(cm^2\right)\)
CM
28 tháng 7 2018
Chọn A.
Do đáy là tam tam giác đều cạnh a nên diện tích đáy là:
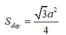
Thể tích khối chóp là:
HT
2
15 tháng 3 2022
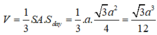
Sorry cho sửa lại
Thể tích hình chóp là: \(V=\dfrac{1}{3}\cdot4\cdot\dfrac{27\sqrt{3}}{4}=9\sqrt{3cm^3}\)
CM
28 tháng 2 2017
Đáp án là A
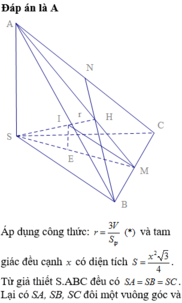
Cách 1. Áp dụng công thức: r = 3 V S t p (*) và tam giác đều cạnh x có diện tích S = x 2 3 4 .
Từ giả thiết S.ABC đều có SA=SB=SC. Lại có SA, SB, SC đôi một vuông góc và thể tích khối chóp S.ABC bằng a 3 6 nên ta có SA=SB=SC=a.
Suy ra AB=BC=CA=a 2 và tam giác ABC đều cạnh có độ dài a 2 . Do đó diện tích toàn phần của khối chóp S.ABC là
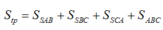
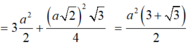
Thay vào (*) ta được:
CM
19 tháng 11 2017
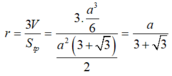
Đáp án A.
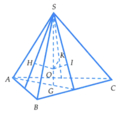
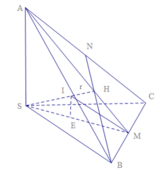
Gọi O là tâm mặt cầu nội tiếp hình chóp.
Gọi G, H, I, K lần lượt là hình chiều vuông góc của O lên ta có
