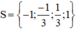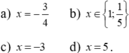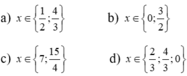giải phương trình: (2x2-3x-1)2-10x2-15x+9=0
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a) 9 x 4 − 10 x 2 + 1 = 0 ( 1 )
Đặt x 2 = t , điều kiện t ≥ 0.
Khi đó (1) trở thành : 9 t 2 − 10 t + 1 = 0 ( 2 )
Giải (2):
Có a = 9 ; b = -10 ; c = 1
⇒ a + b + c = 0
⇒ Phương trình (2) có nghiệm t 1 = 1 ; t 2 = c / a = 1 / 9
Cả hai nghiệm đều thỏa mãn điều kiện.
+ Với t = 1 ⇒ x 2 = 1 ⇒ x = 1 hoặc x = -1.
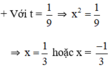
Vậy phương trình (1) có tập nghiệm 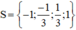
b)
5 x 4 + 2 x 2 - 16 = 10 - x 2 ⇔ 5 x 4 + 2 x 2 - 16 - 10 + x 2 = 0 ⇔ 5 x 4 + 3 x 2 - 26 = 0
Đặt x 2 = t , điều kiện t ≥ 0.
Khi đó (1) trở thành : 5 t 2 + 3 t − 26 = 0 ( 2 )
Giải (2) :
Có a = 5 ; b = 3 ; c = -26
⇒ Δ = 3 2 − 4.5 ⋅ ( − 26 ) = 529 > 0
⇒ Phương trình có hai nghiệm phân biệt
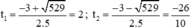
Đối chiếu điều kiện chỉ có t 1 = 2 thỏa mãn
+ Với t = 2 ⇒ ⇒ x 2 = 2 ⇒ x = √2 hoặc x = -√2.
Vậy phương trình (1) có tập nghiệm S = {-√2; √2}
c) 0 , 3 x 4 + 1 , 8 x 2 + 1 , 5 = 0 ( 1 )
Đặt x 2 = t , điều kiện t ≥ 0.
Khi đó, (1) trở thành : 0 , 3 t 2 + 1 , 8 t + 1 , 5 = 0 ( 2 )
Giải (2) :
có a = 0,3 ; b = 1,8 ; c = 1,5
⇒ a – b + c = 0
⇒ Phương trình có hai nghiệm t 1 = − 1 và t 2 = − c / a = − 5
Cả hai nghiệm đều không thỏa mãn điều kiện.
Vậy phương trình (1) vô nghiệm.
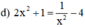
Điều kiện xác định: x ≠ 0.
Quy đồng, khử mẫu ta được :
2 x 4 + x 2 = 1 − 4 x 2 ⇔ 2 x 4 + x 2 + 4 x 2 − 1 = 0 ⇔ 2 x 4 + 5 x 2 − 1 = 0 ( 1 )
Đặt t = x 2 , điều kiện t > 0.
Khi đó (1) trở thành : 2 t 2 + 5 t - 1 = 0 ( 2 )
Giải (2) :
Có a = 2 ; b = 5 ; c = -1
⇒ Δ = 5 2 − 4.2 ⋅ ( − 1 ) = 33 > 0
⇒ Phương trình có hai nghiệm phân biệt:
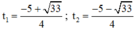
Đối chiếu với điều kiện thấy có nghiệm t 1 thỏa mãn.
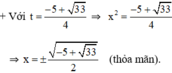
Vậy phương trình có tập nghiệm 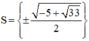

a: =>2x^2+9x-6x-27=0
=>x(2x+9)-3(2x+9)=0
=>(2x+9)(x-3)=0
=>x=3 hoặc x=-9/2
b: =>-10x^2+6x-5x+3=0
=>-2x(5x-3)-(5x-3)=0
=>(5x-3)(-2x-1)=0
=>x=-1/2 hoặc x=5/3
c: =>-x^3+2x^2-x^2+4=0
=>-x^2(x-2)-(x-2)(x+2)=0
=>(x-2)(-x^2-x-2)=0
=>x-2=0
=>x=2
d: =>(x^3+8)-4x(x+2)=0
=>(x+2)(x^2-2x+4)-4x(x+2)=0
=>(x+2)(x^2-6x+4)=0
=>x=-2 hoặc \(x=3\pm\sqrt{5}\)

Ta có: 2 x 2 + 3 2 -10 x 3 -15x =0 ⇔ 2 x 2 + 3 2 - 5x(2 x 2 +3)=0
⇔ (2 x 2 +3)( 2 x 2 +3 - 5x) = 0 ⇔ (2 x 2 +3)( 2 x 2 - 5x +3)=0
Vì 2 x 2 ≥ 0 nên 2 x 2 +3 > 0
Suy ra : 2x2 - 5x +3=0
∆ = - 5 2 -4.2.3 =25 -24=1 > 0
∆ = 1 = 1
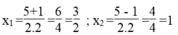
vậy phương trình đã cho có 2 nghiệm: x1 = 3/2 ; x2 = 1

a) 8( 3x - 2 ) - 14x = 2( 4 – 7x ) + 15x
⇔ 24x – 16 -14x = 8 – 14x + 15x
⇔ 10x -16 = 8 + x
⇔ 9x = 24
⇔ x = 24/9
b) ( 3x – 1 )( x – 3 ) – 9 + x2 = 0
⇔ (3x -1)( x – 3) + (x - 3)( x + 3) = 0
⇔ (x - 3)(3x - 1 + x - 3) = 0
⇔ (x - 3)(4x - 4) = 0
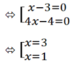
c) |x - 2| = 2x - 3
TH1: x - 2 ≥ 0 ⇔ x ≥ 2
Khi đó: x - 2 = 2x – 3
⇔ 2x – x = -2 + 3
⇔ x = 1 (không TM điều kiện x ≥ 2)
TH2: x – 2 < 0 ⇔ x < 2
Khi đó: x-2 = -(2x – 3)
⇔ x – 2 = -2x + 3
⇔ 3x = 5
⇔ x = 5/3 ( TM điều kiện x < 2)
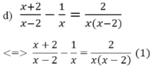
MTC: x(x-2)
ĐKXĐ: x ≠ 0;x ≠ 2

Đối chiếu với ĐKXĐ thì pt có nghiệm x = - 1

Ta có: \(2x^2+3x+\sqrt{2x^2+3x+9}=33\)
\(\Leftrightarrow\left(2x^2+3x-27\right)+\left(\sqrt{2x^2+3x+9}-6\right)=0\)
\(\Leftrightarrow\left(2x+9\right)\left(x-3\right)+\dfrac{2x^2+3x-27}{\sqrt{2x^2+3x+9}+6}=0\)
\(\Leftrightarrow\left(2x+9\right)\left(x-3\right)+\dfrac{\left(2x+9\right)\left(x-3\right)}{\sqrt{2x^2+3x+9}+6}=0\)
\(\Leftrightarrow\left(2x+9\right)\left(x-3\right)\left(1+\dfrac{1}{\sqrt{2x^2+3x+9}+6}\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}2x+9=0\\x-3=0\\1+\dfrac{1}{\sqrt{2x^2+3x+9}+6}=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-\dfrac{9}{2}\\x=3\\1+\dfrac{1}{\sqrt{2x^2+3x+9}+6}=0\left(1\right)\end{matrix}\right.\)
Giải (1) ta có:
\(\left(1\right)\Leftrightarrow\dfrac{1}{\sqrt{2x^2+3x+9}+6}=-1\)
\(\Leftrightarrow1=-\sqrt{2x^2+3x+9}-6\)
\(\Leftrightarrow7=-\sqrt{2x^2+3x+9}\)
\(\Leftrightarrow49=2x^2+3x+9\)
\(\Leftrightarrow2x^2+3x-40=0\)
Ta có:Δ=32-4.2.(-40)=329
Vì Δ>0 nên phương trình có 2 nghiệm phân biệt là:
\(\Rightarrow\left[{}\begin{matrix}x=\dfrac{-b+\sqrt{\Delta}}{2a}=\dfrac{-3+\sqrt{329}}{4}\\x=\dfrac{-b-\sqrt{\Delta}}{2a}=\dfrac{-3-\sqrt{329}}{4}\end{matrix}\right.\)
Vậy phương trình có 4 nghiệm là ....

9x4 – 10x2 + 1 = 0 (1)
Đặt x2 = t, điều kiện t ≥ 0.
Khi đó (1) trở thành : 9t2 – 10t + 1 = 0 (2)
Giải (2):
Có a = 9 ; b = -10 ; c = 1
⇒ a + b + c = 0
⇒ Phương trình (2) có nghiệm t1 = 1; t2 = c/a = 1/9.
Cả hai nghiệm đều thỏa mãn điều kiện.
+ Với t = 1 ⇒ x2 = 1 ⇒ x = 1 hoặc x = -1.
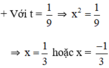
Vậy phương trình (1) có tập nghiệm