Rút gọn tổng: S = 1 + 2.3 + 3.32 + 4.33 +....+101.3100
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Chọn C.
Từ giả thiết suy ra 3S = 3 + 2.32 + 3.33 + … + 11.311. Do đó
-2S = S – 3S = 1 + 3 + 32 + … + 310 – 10.311
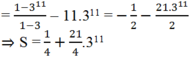
Vì 
![]()

Chọn C
Từ giả thiết suy ra 3 S = 3 + 2.3 2 + 3.3 3 + ... + 11.3 11 . Do đó
− 2 S = S − 3 S = 1 + 3 + 3 2 + ... + 3 10 − 11.3 11 = 1. 1 − 3 11 1 − 3 − 11.3 11 = − 1 2 − 21.3 11 2 ⇒ S = 1 4 + 21 4 .3 11 .
vì
S = 1 4 + 21.3 11 4 = a + 21.3 b 4 ⇒ a = 1 4 , b = 11 ⇒ P = 1 4 + 11 4 = 3.

Trả lời :
\(\frac{42}{15.7}\)= \(\frac{2.3.7}{3.5.7}\)= \(\frac{2}{5}\)
\(\frac{4.33}{11.12}\)= \(\frac{4.3.11}{11.3.4}\)= \(1\)
_Học tốt
\(\frac{42}{15.7}=\frac{3.2.7}{3.5.7}=\frac{2}{5}\)
\(\frac{36.6}{336}=\frac{3.4.3.3.2}{2.4.2.3.7}=\frac{3.3}{2.7}=\frac{9}{14}\)
\(\frac{4.33}{11.12}=\frac{4.11.3}{11.3.4}=1\)



\(\frac{2^2.3^3.35}{2^4.3^2.21}=\frac{2^2.3^2.3.35}{2^2.2^2.3^2.21}=\frac{3.35}{2^2.21}=\frac{3.35}{2^2.3.7}=\frac{35}{2^2.7}=\frac{35}{28}=\frac{5}{4}\)

1.4./x-5/-54=-34
4./x-5/=-34+54
4./x-5/=20
/x-5/=20:4
/x-5/=5
=>x-5=5 va x-5=-5
TH1:x-5=-5
=>x=0
TH2:x-5=5
=>x=10
2. /x-1/+(-5)=2
/x-1/=2-(-5)
/x-1/=7
=>x-1=7 va x-1=-7
TH1: x-1=7
=>x=8
TH2:x-1=-7
=>x=-6
vay x=-6 hoac x=8
3S= 3+2.32+3.33+...+101.3101
<=> 2S= 101.3101-(3100+399+398+....+3)-1 (1)
Ta có
A=3100+399+...+3
<=> 3A=3101+3100+...+32
<=> A=\(\frac{3^{101^{ }}-3}{2}\)(2)
Thay (2) vào (1) ta có
S= \(\frac{101.3^{101}-\frac{3^{101}-3}{2}-1}{2}\)
<=> S=\(\frac{3^{101}.201-1}{2}.\frac{1}{2}\)=\(\frac{3^{101}.201-1}{4}\)
Mik nghĩ vậy k bt đúng k