tìm hai số tự nhiên biết hiệu của số lớn vói số nhỏ bằng 1814 và khi chia số lớn cho số nhỏ thì được 9 và dư 182
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
25 tháng 4 2018
Theo đề bài ta có :
số lớn - số bé = 1814 => số lớn = 1814 + số bé
( số lớn - 182 ) / số bé = 9 => số lớn - 182 = 9 x số bé
Nên => 1814 + số bé - 182 = 9 x số bé
=> 8 x số bé = 1632 => số bé = 204
=> số lớn = 1814 + 204 = 2018
Vậy số bé là 204
số lớn là 2018
AH
Akai Haruma
Giáo viên
11 tháng 7 2021
Lời giải:
Gọi số lớn là $a$ và số bé là $b$. Theo bài ra ta có:
$a-b=578(1)$
$a=8b+53$. Thay vô $(1)$ thì:
$8b+53-b=578$
$7b+53=578$
$7b=525$
$b=75$
$a=578+b=578+75=653$
12 tháng 11 2017
Hiệu mới sẽ là:57-9=48
Hiệu số phần bằng nhau là:2-1=1
Số lớn là:48:1x2+9=105
Số bé là:48:1x1=48
Đáp số:Số lớn:105
Số bé:48
12 tháng 11 2017
Giá trị 1 phần hay số bé là : (57-9):2=24
Số lớn là : 24x2+9=57
Đáp số :số lớn 57
số bé là 24
CM
13 tháng 6 2017
Gọi số lớn là x, số nhỏ là y (x, y ∈ N*); x,y > 124.
Tổng hai số bằng 1006 nên ta có: x + y = 1006
Số lớn chia số nhỏ được thương là 2, số dư là 124 nên ta có: x = 2y + 124.
Ta có hệ phương trình:
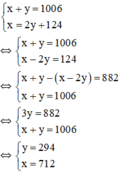
Vậy hai số tự nhiên phải tìm là 712 và 294.
Chú ý : Số bị chia = số chia. thương + số dư
CM
19 tháng 10 2017
Gọi số lớn là x, số nhỏ là y (x, y ∈ N*); x,y > 124.
Tổng hai số bằng 1006 nên ta có: x + y = 1006
Số lớn chia số nhỏ được thương là 2, số dư là 124 nên ta có: x = 2y + 124.
Ta có hệ phương trình:
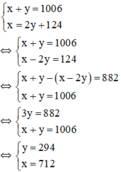
Vậy hai số tự nhiên phải tìm là 712 và 294.
Chú ý : Số bị chia = số chia. thương + số dư
Kiến thức áp dụng
Giải bài toán bằng cách lập hệ phương trình:
Bước 1: Lập hệ phương trình
- Chọn các ẩn số và đặt điều kiện thích hợp
- Biểu diễn các đại lượng chưa biết và đã biết theo ẩn
- Lập các phương trình biểu thị mối quan hệ giữa các đại lượng theo đề bài.
- Từ các phương trình vừa lập rút ra được hệ phương trình.
Bước 2: Giải hệ phương trình (thường sử dụng phương pháp thế hoặc cộng đại số).
Bước 3: Đối chiếu nghiệm với điều kiện và kết luận.