Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
a/ Xét tg HBA và tg ABC, có:
góc BHA = góc BAC = 90 độ
góc B chung
Suyra: tg HBA đồng dạng với tg ABC (g-g)
b/ Ta có tg ABC vuông tại A:
\(BC^2=AC^2+AB^2\)
\(BC^2=8^2+6^2=100\)
\(\Rightarrow BC=\sqrt{100}=10\)(cm)
Ta có: \(\frac{HA}{AC}=\frac{BA}{BC}\)(tg HBA đồng dạng với tg ABC)
\(\Rightarrow\frac{HA}{8}=\frac{6}{10}\)
\(\Rightarrow HA=\frac{8.6}{10}=4,8\left(cm\right)\)
a)Xét tam giác ABC vuông tại A(gt),có:
AB^2+AC^2=BC^2(Đl pytago)
Thay số:36+64=BC^2
=>BC= căn 100=10cm
Xét tam giác ABC có BD là phân giác góc ABC(gt),có:
AB/AC=AD/DC(Tính chất đường phân giác trong tam giác)
<=>AB/AB+AC=AD/AD+DC(Tính chất tỉ lệ thức)
Thay số:6/16=AD/8
<=>16AD=48
<=>AD=3cm
Vì D thuộc AC(gt)
=>AD+DC=AC
Thay số:3+DC=8
<=>DC=5cm
b) Xét tam giác ABC vuông tại A(gt),có:
SABC=(AB.AC)/2=24cm^2
Mà SABC=(AH.BC)/2
=>(AH.10)/2=24
<=>AH=24.2÷10=4,8cm
Xét tam giác ABC đồng dạng tam giác HAC có:
+Góc C chung
+Góc AHC=góc BAC=90 độ
=>tam giác ABC đồng dạng tam giác HAC(g.g)
=> AH/AB=CH/AC(Cặp cạnh tương ứng)
Thay số : 4,8/6=CH/8
=>CH=4,8.8÷6=6,4cm
c)
b) Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow BC^2=3^2+4^2=25\)
hay BC=5(cm)
Ta có: ΔHBA\(\sim\)ΔABC(cmt)
nên \(\dfrac{BA}{BC}=\dfrac{HB}{AB}=\dfrac{AH}{CA}\)(Các cặp cạnh tương ứng tỉ lệ)
hay \(\dfrac{HB}{3}=\dfrac{3}{5}=\dfrac{AH}{4}\)
\(\Leftrightarrow\left\{{}\begin{matrix}HB=\dfrac{9}{5}=1.8\left(cm\right)\\AH=\dfrac{12}{5}=2.4\left(cm\right)\end{matrix}\right.\)
Vậy: BC=5cm; AH=2,4cm; HB=1,8cm
a) Xét ΔHBA vuông tại H và ΔABC vuông tại A có
\(\widehat{B}\) chung
Do đó: ΔHBA\(\sim\)ΔABC(g-g)
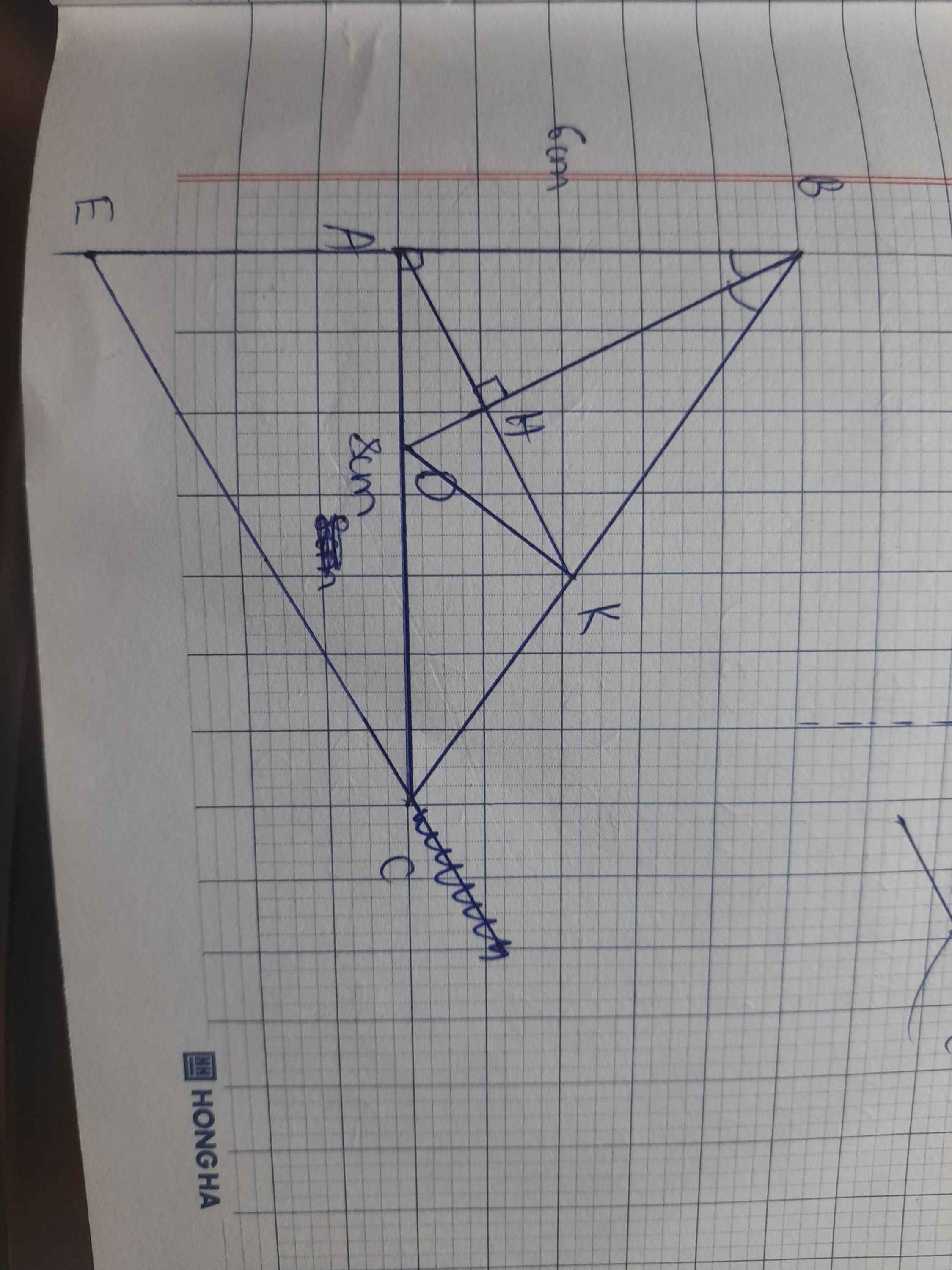
Bài trên là câu e) của bài làm các câu còn lại (đã làm)gồm:
A)Chứng minh[CM] \(\Delta ABC\)đồng dạng \(\Delta HBA\)
b)Tính BC, HB, HC
c) Tính diện tích \(\Delta ABC\)
d) CM AH2 =HB.HC
e) Tia phân giác.......(phần trên mình có ghi)
MONG GIÚP ĐỠ THỨ 2 LÀ GIẢI RỒI, LÀM GIÚP MÌNH NHA, CHƯA HIỂU CÂU (E) CHO LẮM