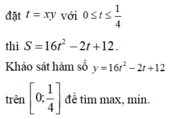Với x>0 tìm giá trị nhỏ nhất của M = 4x2-3x+\(\frac{1}{4x}\)+2019
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NK
0
NT
1
I
2 tháng 3 2020
\(M=\)như trên
\(=>M=4x^2-4x+1+x+\frac{1}{4x}+2010\)
\(=>M=\left(4x^2-4x+1\right)+\left(x+\frac{1}{4x}\right)+2010\)
\(=>M=\left(2x-1\right)^2+\left(x+\frac{1}{4x}\right)+2010\)
Áp dụng BĐT Cô- si cho 2 số không âm, ta có:
\(x+\frac{1}{4x}\ge2\sqrt{x.\frac{1}{4x}}=2\sqrt{\frac{1}{4}}=1\)
\(=>M=\left(2x-1\right)^2+\left(x+\frac{1}{4x}\right)+2010\ge0+1+2010=2011\\ \)
=>minM=2011 khi x=\(\frac{1}{2}\)
CM
12 tháng 10 2019
Đáp án B
Từ giả thiết
2017 1 − y 2017 x = x 2 + 2018 1 − y 2 + 2018 ⇔ 2017 1 − y 1 − y 2 + 2018 = 2017 x x 2 + 2018 *
Xét hàm số f t = 2017 t t 2 + 2018 với t ∈ 0 ; 1
⇒ f ' t = 2017 t ln 2017 t 2 + 2018 + 2 t .2017 t > 0
⇒ f t đồng biến trên 0 ; 1 . Do đó (*) ⇔ 1 − y = x ⇔ x + y = 1.
Ta có: 0 ≤ x y ≤ x + y 2 4 = 1 4 . Đặt m = x y ∈ 0 ; 1 4 . Khi đó :
S = 16 x 2 y 2 + 34 x y + 12 y + x y + x 2 − 3 x y = 16 m 2 − 2 m + 12 = g m
Xét hàm g m trên đoạn
0 ; 1 4 ⇒ g ' m = 32 m − 2 → g ' m = 0 ⇔ m = 1 16
Lúc này
g 0 = 12 , g 1 4 = 25 2 , g 1 16 = 191 16 ⇒ M = 25 2 m = 191 16 ⇒ M + m = 391 16 .
CM
15 tháng 2 2017
Đáp án B
Từ giả thiết
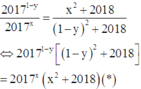
Xét hàm số
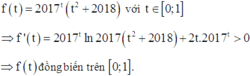
Do đó (*)
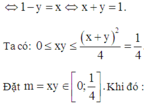
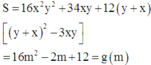
Xét hàm g(m) trên đoạn
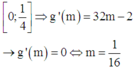
Lúc này
CM
18 tháng 12 2018
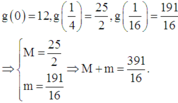
Đáp án B
Ta có 2017 1 − x − y = x 2 + 2018 y 2 − 2 y + 2019 ⇔ 2017 1 − y 2017 x = x 2 + 2018 1 − y 2 + 2018
2017 x x 2 + 2018 = 2017 1 − y 1 − y 2 + 2018 ⇔ f x = f 1 − y
Xét hàm số f t = 2017 t t 2 + 2018 = t 2 .2017 t + 2018.2017 t , có
f ' t = 2 t .2017 t + t 2 .2017 t . ln 2017 + 2018.2017 t . ln 2017 > 0 ; ∀ t > 0
Suy ra f(t) là hàm đồng biến trên 0 ; + ∞ mà f x = f 1 − y ⇒ x + y = 1
Lại có P = 4 x 2 + 3 y 4 y 2 + 3 x + 25 x y = 16 x 2 y 2 + 12 x 3 + 12 y 3 + 34 x y
16 x 2 y 2 + 12 x + y 3 − 3 x y x + y + 34 x y = 16 x 2 y 2 + 12 1 − 3 x y + 34 x y = 16 x 2 y 2 − 2 x y + 12
Mà 1 = x + y ≥ 2 x y ⇔ x y ≤ 1 4 nên đặt t = x y ∈ 0 ; 1 4 khi đó P = f t = 16 t 2 − 2 t + 12
Xét hàm số f t = 16 t 2 − 2 y + 12 trên 0 ; 1 4 ta được min 0 ; 1 4 f t = f 1 16 = 191 16 max 0 ; 1 4 f t = f 1 4 = 25 2
HT
2
T
1 tháng 1 2020
Lâu rồi không show cách này:)
Sửa đề: \(M=4x^2-3x+\frac{1}{4x}+2017\)
Ta có: \(M=\frac{\left(4x+1\right)\left(2x-1\right)^2}{4x}+2017\ge2017\)
Đẳng thức xảy ra khi \(x=\frac{1}{2}\)
31 tháng 12 2019
Em kiểm tra lại đề nhé! Hàm số của biểu thức : \(M=4^2-3x+\frac{1}{4x}+2017\) có đồ thị đi xuống nên sẽ không tồn tại GTNN em nhé!
NT
1
AH
Akai Haruma
Giáo viên
2 tháng 3 2020
Lời giải:
Áp dụng BĐT AM-GM cho các số dương ta có:
$3x^2+\frac{3}{4}\geq 3x$
$x^2+\frac{1}{8x}+\frac{1}{8x}\geq 3\sqrt[3]{x^2.\frac{1}{8x}.\frac{1}{8x}}=\frac{3}{4}$
Cộng theo vế:
$\Rightarrow 4x^2+\frac{1}{4x}+\frac{3}{4}\geq 3x+\frac{3}{4}$
$\Rightarrow 4x^2+\frac{1}{4x}\geq 3x$
$\Rightarrow M=4x^2+\frac{1}{4x}-3x+2011\geq 2011$
Vậy $M_{\min}=2011$ khi $x=\frac{1}{2}$
DQ
1
9 tháng 8 2016
(4x2 -4x+1) + (x+ \(\frac{1}{4x}\)-2)+ 2016=(2x-1)2 +(√x -√ \(\frac{1}{4x}\))2 >=2016 đạt giá trị nhỏ nhất khi x=0,5