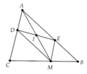
Cho tam giác nhọn ABC, điểm M di chuyển trên cạnh BC (M không trùng B và C). Qua M kẻ các đường thẳng song song với AC và AB, các đường thẳng này cắt AC và AB thứ tự tại D và E. Xác định vị trí của M sao cho tứ giác ADME có diện tích lớn nhất.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
22 tháng 11 2017
Chứng minh được ADME là hình bình hành Þ I là trung điểm của AM. Tương tự 2A. I thuộc đường trung bình của D ABC (đường thẳng đi qua trung điểm của AB và AC)
KA
7 tháng 11 2021
1) ADME là h.b.h (vì có 2 cặp cạnh đối song song)
2) Vì ADME là hình chữ nhật nên O là trung điểm 2 đường chéo AM và DE.
Xét tam giác AHM vuông tại H, đường trung tuyến HO, khi đó HO = AO = OM
Vậy tam giác AHO cân ở O
3)
a, Tam giác ABC vuông tại A nên ˆDAE=900DAE^=900
Mà ADME là h.b.h nên tứ giác ADME là hình chữ nhật
b, Vì tứ giác AEMD là hình chữ nhật nên ED=AM
Để DE có độ dài nhỏ nhất thì AM có độ dài nhỏ nhất hay M là chân đường vuông góc hạ từ A xuống BC
NX
5 tháng 9 2023
Ta đặt: \(S_{BEMF}=S_1;S_{ABC}=S\)
Kẻ \(AK\perp BC\) ; \(AK\) cắt \(EM\left\{H\right\}\)
Ta có: \(S_1=EM.HK\)
\(\Leftrightarrow S=\dfrac{1}{2}BC.AK\)
\(\Leftrightarrow\dfrac{S_1}{S}=2\dfrac{EM}{BC}.\dfrac{KH}{AK}\)
Đặt \(MA=x;MC=y\) . Theo định lý Thales ta có:
\(\dfrac{EM}{BC}=\dfrac{x}{x+y};\dfrac{HK}{AK}=\dfrac{x}{x+y}\)
\(\Leftrightarrow\dfrac{S_1}{S}=\dfrac{2xy}{\left(x+y\right)^2}\)
Áp dụng bất đẳng thức Cosi dạng \(\dfrac{ab}{\left(a+b\right)^2}\le\dfrac{1}{4}\) ta được:
\(\dfrac{S_1}{S}=\dfrac{2xy}{\left(x+y\right)^2}\le\dfrac{1}{2}\) hay \(S_1\le\dfrac{1}{2}S\)
\(\Leftrightarrow MaxS_1=\dfrac{1}{2}S\)
\(\Leftrightarrow\) \(M\) là trung điểm của \(AC\)
5 tháng 8 2018
a, \(MD//AB,AB\perp AC\left(gt\right)\Rightarrow MD\perp AC\Rightarrow\widehat{MDA}=90^0\)
\(ME//AC,AB\perp AC\left(gt\right)\Rightarrow ME\perp AB\Rightarrow\widehat{MEA}=90^0\)
Tứ giác MDAE có 3 góc vuông nên là hình chữ nhật.
b, Hình chữ nhật có 1 đường chéo là đường phân giác thì là hình vuông
Do đó: \(MDAE\) là hình vuông \(\Leftrightarrow\) AM là tia phân giác của \(\widehat{DAE}\)
Vậy M là giao điểm giữa tia p/g của \(\widehat{DAE}\) và cạnh BC thì MDAE là hình vuông.
c, MDAE là hình chữ nhật (cmt) \(\Rightarrow DE=AM\) (tính chất của HCN)
AM ngắn nhất khi AM là đường cao.
Vậy DE ngắn nhất khi AM là đường cao của \(\Delta ABC.\)
Chúc bạn học tốt.
3 tháng 2 2022
a: Xét tứ giác AFME có
MF//AE
ME//AF
Do đó: AFME là hình bình hành
mà \(\widehat{FAE}=90^0\)
nên AFME là hình chữ nhật
b: Để AFME là hình vuông thì AM là tia phân giác của góc FAE
Vậy: Khi M là chân đường phân giác kẻ từ A đến BC thì AFME là hình vuông