a+b=1 chứng tỏ a2+b2>=1/2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
TC
1
NV
Nguyễn Việt Lâm
Giáo viên
3 tháng 5 2019
a/
Do \(\left\{{}\begin{matrix}a>2\Rightarrow\frac{1}{a}< \frac{1}{2}\\b>2\Rightarrow\frac{1}{b}< \frac{1}{2}\end{matrix}\right.\) \(\Rightarrow\frac{1}{a}+\frac{1}{b}< \frac{1}{2}+\frac{1}{2}=1\)
\(\Rightarrow\frac{a+b}{ab}< 1\Rightarrow a+b< ab\) (đpcm)
b/ Ko rõ đề là gì
c/ \(\frac{a^2+b^2}{2}\ge ab\Leftrightarrow a^2+b^2\ge2ab\)
\(\Leftrightarrow a^2-2ab+b^2\ge0\Leftrightarrow\left(a-b\right)^2\ge0\) (luôn đúng)
Vậy BĐT được chứng minh
18 tháng 1 2018
với a = b thì a - b = 0
ở bước (a+b)(a-b)=b(a-b) sang bước suy ra a+b=b bn đã chia cả hai vế cho a-b=0 là không được
Vậy chỗ sai là không có phép chia cho 0 đâu nhé
P/s: Mk chưa học tới lớp 9, nếu sai mong bn thông cảm. :))
TP
26 tháng 9 2018
chữ " b" mk ghi ở phần b) trước "CMR " là gõ nhầm đấy, ko liên quan j đến bài toán đâu !!
NT
0
CM
16 tháng 1 2019
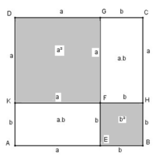
Dựng hình vuông ABCD có cạnh bằng a
Trên cạnh AB lấy điểm E sao cho BE = b
Từ E dựng đường thẳng song song BC cắt CD tại G
Ta có: CG = b, CE = ( a – b ), GD = ( a – b )
Trên cạnh AD lấy điểm K sao cho AK = b
Từ K kẻ đường thẳng song song với AB cắt BC tại H và cắt EG tại F
Ta có: KD = ( a – b ), BH = b
Hình vuông ABCD có diện tích bằng a 2
Hình vuông DKFG có diện tích bằng a - b 2
Hình chữ nhật AEFK có diện tích bằng ( a – b ) b
Hình vuông EBHF có diện tích bằng b 2
Hình chữ nhật HCGF có diện tích bằng ( a – b ).b
S A B C D = S D K F G + S A E F K = S E B H F + S H C G F
nên a - b 2 + a - b b + a - b b + b 2 = a 2
⇒ a - b 2 = a 2 - 2 a b + b 2
DT
Dang Tung
CTVHS
12 tháng 6 2023
Sửa đề : \(\dfrac{a^2}{a^2+b}+\dfrac{b^2}{b^2+a}\le1\\ \) (*)
\(< =>\dfrac{a^2\left(b^2+a\right)+b^2\left(a^2+b\right)}{\left(a^2+b\right)\left(b^2+a\right)}\le1\\ < =>a^2b^2+a^3+b^2a^2+b^3\le\left(a^2+b\right)\left(b^2+a\right)\) ( Nhân cả 2 vế cho `(a^{2}+b)(b^{2}+a)>0` )
\(< =>a^3+b^3+2a^2b^2\le a^2b^2+b^3+a^3+ab\\ < =>a^2b^2\le ab\\ < =>ab\le1\) ( Chia 2 vế cho `ab>0` )
Do a,b >0
Nên áp dụng BDT Cô Si :
\(2\ge a+b\ge2\sqrt{ab}< =>\sqrt{ab}\le1\\ < =>ab\le1\)
Do đó (*) luôn đúng
Vậy ta chứng minh đc bài toán
Dấu "=" xảy ra khi : \(a=b>0,a+b=2< =>a=b=1\)
LD
22 tháng 7 2023
a Sửa đề : Chứng minh \(\dfrac{a^2}{a^2+b}\)+\(\dfrac{b^2}{b^2+a}\)\(\le\) 1 ( Đề thi vào 10 Hà Nội).
Bất đẳng thức trên tương đương :
\(\dfrac{a^2+b-b}{a^2+b}\)+\(\dfrac{b^2+a-a}{b^2+a}\)\(\le\)1
\(\Leftrightarrow\) 1 - \(\dfrac{b}{a^2+b}\)+ 1 - \(\dfrac{a}{b^2+a}\)\(\le\)1
\(\Leftrightarrow\)1 - \(\dfrac{b}{a^2+b}\) - \(\dfrac{a}{b^2+a}\)\(\le\)0
\(\Leftrightarrow\)- \(\dfrac{b}{a^2+b}\)- \(\dfrac{a}{b^2+a}\)\(\le\)-1
\(\Leftrightarrow\)\(\dfrac{a}{b^2+a}\)+ \(\dfrac{b}{a^2+b}\)\(\ge\)1
Xét VT = \(\dfrac{a^2}{ab^2+a^2}\)+ \(\dfrac{b^2}{a^2b+b^2}\)\(\ge\)\(\dfrac{\left(a+b\right)^2}{ab^2+a^2+a^2b+b^2}\) (Cauchy - Schwarz)
= \(\dfrac{\left(a+b\right)^2}{ab\left(b+a\right)+a^2+b^2}\)
\(\ge\)\(\dfrac{\left(a+b\right)^2}{2ab+a^2+b^2}\)
= \(\dfrac{\left(a+b\right)^2}{\left(a+b\right)^2}\)= 1
Vậy BĐT được chứng minh
Dấu '=' xảy ra \(\Leftrightarrow\)a = b = 1
với mọi a, b ta có :
( a - b) ² >= 0
<=> a² - 2ab + b² >= 0
<=> a² + b² >=2ab
<=> 2 ( a² + b² ) >= a² +2ab + b²
<=> 2 (a² + b² ) >= ( a + b )² mà a+b=1 nên 2 ( a² + b² ) >=1
<=> a² + b² >= 1/2
Dấu “ = " xảy ra khi và chỉ khi : a=b mà a+b=1 nên a=b=1/2
nhớ k nha