x/11=y/12;y/3=z/7 và 2x+y-z=152
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
TB
3
TT
1
10 tháng 4 2022
|x-y|=12
=>x-y=12 hoặc x-y=-12
=>x=y+12 hoặc x=y-12
\(\dfrac{x-11}{y-10}=\dfrac{11}{10}\)
=>10x-110=11y-110
=>10x-11y=0(1)
Trường hợp 1: x=y+12
(1)=> 10(y+12)-11y=0
=>10y+120-11y=0
=>y=120
=>x=132
Trường hợp 2: x=y-12
(1) =>10(y-12)-11y=0
=>y=-120
=>x=-132
CM
29 tháng 1 2017
Đáp án B
Mặt cầu S : x - 1 2 + y + 1 2 + z 2 = 11 có tâm I(1;-1;0) bán kính R= 11
Các đường thẳng d 1 , d 2 có vectơ chỉ phương lần lượt là:
Mặt phẳng α song song với d 1 , d 2 có vectơ pháp tuyến là:
α có dạng: α : 3x-y-z+d=0. Vì α tiếp xúc với (S ) nên: d(I; α )=R
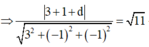
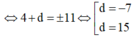
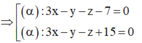
Nhận thấy điểm A(5;-1;1) ∈ d 1 cũng thuộc vào mặt phẳng 3x-y-z+15=0 =>mặt phẳng này chứa d 1
Vậy phương trình mặt phẳng α thỏa mãn yêu cầu bài toán là: α : 3x-y-z+7=0
NB
1
QT
1
HQ
Hà Quang Minh
Giáo viên
18 tháng 9 2023
Áp dụng tính chất của dãy tỉ số bằng nhau, ta có:
\(\begin{array}{l}\dfrac{x}{{11}} = \dfrac{y}{{17}} = \dfrac{{x - y}}{{11 - 17}} = \dfrac{{12}}{{ - 6}} = - 2\\ \Rightarrow x = ( - 2).11 = - 22\\y = ( - 2).17 = - 34\end{array}\)
Vậy \(x = -22; y = -34\).
