Bạn Hà đi từ A đến B dài 120km trong thời gian đã định. Nhưng đi được 1 giờ Hà nghỉ 10 phút nên để đến B đúng giờ, thì sau đó Hà phải tăng vận tốc thêm 6km/h nữa. Tính vận tốc lúc đầu?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Quãng đường đi được trong 2 giờ là : 40 x 2 = 80 ( km )
1/2 giờ người đi được là : 40 x 1/2 = 20 ( km )
Mỗi giờ sau khi giải lao sẽ tăng 10 km = > Số giờ để người đó đi đến Hà Nội là : 20 : 10 = 2 ( giờ )
Đoạn đường từ quê ra HN là : 80 + (40 +10 ) x 2 = 180 ( km )
ĐS : ......

Gọi vận tốc lúc đầu là x km/h. Vận tốc lúc sau là: x + 6 km/h.
Thời gian đự định đi là: \(\frac{120}{x}\)
Quãng đường đi với vận tốc ban đầu là: x
Quãng đường đi với vận tốc sau là: \(120-x\)
Thời gian đi quãng đường sau là: \(\frac{120-x}{x+6}\)
Theo đề bài thì ta có:
\(\frac{120}{x}=1+\frac{1}{6}+\frac{120-x}{x+6}\)
\(\Leftrightarrow\orbr{\begin{cases}x=-90\left(l\right)\\x=48\end{cases}}\)

Đáp án C
* Phân tích:
Ta luôn có: Quãng đường = vận tốc . thời gian
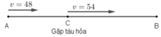
Gọi C là địa điểm ô tô gặp tàu hỏa.
Quãng đường AC ô tô đi với vận tốc 48km/h trong 1h nên SAC = 48km.
Xét trên quãng đường BC, để đến B đúng thời gian đã định ô tô đi với vận tốc 48 + 6 = 54 (km/h).
Vì ô tô đến B đúng thời gian đã định nên thời gian thực tế ô tô đi từ B đến C ít hơn thời gian dự định là 10 phút = 1/6 giờ (là thời gian chờ tàu hỏa).
| Quãng đường BC | Vận tốc | Thời gian | |
| Dự tính | x | 48 | 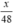 |
| Thực tế | x | 48 + 6 = 54 | 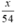 |
Ta có phương trình: 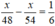
* Giải:
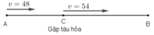
Gọi C là địa điểm ô tô gặp tàu hỏa.
Quãng đường AC ô tô đi với vận tốc 48km/h và đi trong 1 giờ
⇒ SAC = 48.1 = 48 (km).
Gọi quãng đường BC dài là x (km; x > 0).
Vận tốc dự tính đi trên BC là: 48 km/h
⇒ Thời gian dự tính đi quãng đường BC hết: 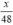 (giờ).
(giờ).
Thực tế ô tô đi quãng đường BC với vận tốc bằng 48 + 6 = 54 (km/h).
⇒ Thời gian thực tế ô tô đi quãng đường BC là: 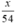 (giờ).
(giờ).
Thời gian chênh nhau giữa dự tính và thực tế chính là thời gian ô tô đợi tàu hỏa là 10 phút = 1/6 (giờ).
Do đó ta có phương trình:
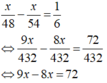
⇔ x = 72 (thỏa mãn) nên quãng đường BC là 72 (km).
Vậy quãng đường AB là:
SAB = SAC + SBC = 48 + 72 = 120 (km).

* Phân tích:
Ta luôn có: Quãng đường = vận tốc . thời gian
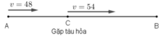
Gọi C là địa điểm ô tô gặp tàu hỏa.
Quãng đường AC ô tô đi với vận tốc 48km/h trong 1h nên SAC = 48km.
Xét trên quãng đường BC, để đến B đúng thời gian đã định ô tô đi với vận tốc 48 + 6 = 54 (km/h).
Vì ô tô đến B đúng thời gian đã định nên thời gian thực tế ô tô đi từ B đến C ít hơn thời gian dự định là 10 phút = 1/6 giờ (là thời gian chờ tàu hỏa).
| Quãng đường BC | Vận tốc | Thời gian | |
| Dự tính | x | 48 | 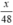 |
| Thực tế | x | 48 + 6 = 54 | 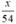 |
Ta có phương trình: 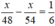
* Giải:
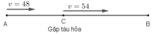
Gọi C là địa điểm ô tô gặp tàu hỏa.
Quãng đường AC ô tô đi với vận tốc 48km/h và đi trong 1 giờ
⇒ SAC = 48.1 = 48 (km).
Gọi quãng đường BC dài là x (km; x > 0).
Vận tốc dự tính đi trên BC là: 48 km/h
⇒ Thời gian dự tính đi quãng đường BC hết: 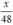 (giờ).
(giờ).
Thực tế ô tô đi quãng đường BC với vận tốc bằng 48 + 6 = 54 (km/h).
⇒ Thời gian thực tế ô tô đi quãng đường BC là: 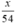 (giờ).
(giờ).
Thời gian chênh nhau giữa dự tính và thực tế chính là thời gian ô tô đợi tàu hỏa là 10 phút = 1/6 (giờ).
Do đó ta có phương trình:
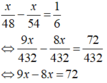
⇔ x = 72 (thỏa mãn) nên quãng đường BC là 72 (km).
Vậy quãng đường AB là:
SAB = SAC + SBC = 48 + 72 = 120 (km).

Gọi vận tốc của Ô tô lúc đầu là x (km/h). Điều kiện: 0 < x <120
Vận tốc của Ô tô lúc sau là: x + 6 (km/h)
Thời gian dự định đi là: \(\frac{120}{x}\)(h)
Quảng đường Ô tô đi trong 1 giờ là 1.x = x (km)
Quảng đường còn lại là: 120 – x (km)
Thời gian Ô tô đi trên quảng đường còn lại là: \(\frac{120-x}{x+6}\)(h)
Vì thời gian dự định đi bằng thời gian đi trên thực tế nên ta có phương trình:
\(\frac{120}{x}\) = 1 + \(\frac{1}{6}\) + \(\frac{120-6}{x+6}\)
==> x= 48 (km/h)

Bài 1:
Đổi 10 phút thành 1/6 giờ
Thời gian đi dự định: $\frac{AB}{48}$ (h)
Thời gian đi thực tế: $1+\frac{1}{6}+\frac{AB-48}{48+6}$
$=\frac{7}{6}+\frac{AB-48}{54}$ (h)
Ta có: $\frac{AB}{48}=\frac{7}{6}+\frac{AB-48}{54}$
$\Leftrightarrow \frac{AB}{432}=\frac{5}{18}$
$\Rightarrow AB=120$ (km)
Bài 2:
Đổi 1h40 phút thành $\frac{5}{3}$ giờ, đổi 20 phút thành $\frac{1}{3}$ giờ
Thời gian dự định đi: $\frac{AB}{12}$ (giờ)
Thời gian thực tế: \(\frac{AB}{3.12}+\frac{1}{3}+\frac{2AB}{3.36}=\frac{5AB}{108}+\frac{1}{3}\) (giờ)
Theo bài ra:
$\frac{5AB}{108}+\frac{1}{3}+\frac{5}{3}=\frac{AB}{12}$
$\Leftrightarrow AB=54$ (km)

Đổi: 10 phút = 1/6 (giờ)
Gọi vận tốc lúc đầu là V (km/h)
=> Thời gian dự định là: 120/V (giờ)
Sau 1 giờ thì Hà đi được quãng đường là: V*1=V (km)
Quãng đường còn lại là: 120-V (km)
Vận tốc khi tăng lên là: V+6 (km/h)
Thời gian đi hết quãng đường còn lại là: \(\frac{120-V}{V+6}\)
Theo bài ra ta có: \(\frac{120-V}{V+6}+\frac{1}{6}+1=\frac{120}{V}\)<=> \(\frac{120-V}{V+6}+\frac{7}{6}=\frac{120}{V}\)
<=> 6V(120-V)+7V(V+6)=120.6.(V+6)
<=> 720V-6V2+7V2+42V-720V-4320=0
<=> V2+42V-4320=0
<=> V2-48V+90V-4320=0
<=> V(V-48)+90(V-48)=0
<=> (V-48)(V+90)=0
=> V=48 (V=-90 loại)
Đáp số: Vận tốc ban đầu là 48km/h