Cho 𝛥 ABC có 3 góc nhọn (AB < AC), M là trung điểm của AC. Trên tia đối của tia MB lấy điểm D sao cho BM = MD.
a) Chứng minh 𝛥 ABM = 𝛥 CDM
b) Chứng minh AB // CD.
c) Vẽ AH, CK vuông góc với BD (K, H thuộc BD). Chứng minh BH = DK
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét ΔABM và ΔCDM có
MA=MC
\(\widehat{AMB}=\widehat{CMD}\)
MB=MD
Do đó: ΔABM=ΔCDM
b: ΔABM=ΔCDM
=>\(\widehat{MAB}=\widehat{MCD}=90^0\)
=>DC\(\perp\)AC
mà AC\(\perp\)AB
nên AB//DC
c: ΔMAB=ΔMCD
=>AB=CD
Xét ΔKAB và ΔKEC có
KA=KE
\(\widehat{AKB}=\widehat{EKC}\)
KB=KC
Do đó: ΔKAB=ΔKEC
=>AB=EC
ΔKAB=ΔKEC
=>\(\widehat{KAB}=\widehat{KEC}\)
mà hai góc này là hai góc ở vị trí so le trong
nên AB//EC
AB//EC
AB//CD
CD,EC có điểm chung là C
Do đó: E,C,D thẳng hàng
AB=EC
AB=CD
Do đó: EC=CD
Ta có: E,C,D thẳng hàng
EC=CD
Do đó: C là trung điểm của ED

a: Xét tứ giác ABCD có
M là trung điểm chung của AC và BD
nên ABCD là hình bình hành
=>AB//CD
=>góc ABM=góc CDM
b: Vì ABCD là hình bình hành
nên AB=CD
AB//CD
AB vuông góc với AC
Do đó: CD vuông góc với AC
=>AC vuông góc với DE
c: Xét tứ giác ABEC có
CE//AB
BE//AC
Do đó: ABEC là hình bình hành
=>CE=AB=CD
=>C là trung điểm của ED

a: Xét ΔABM và ΔCDM có
MA=MC
góc AMB=góc CMD
MB=MD
Do đó: ΔABM=ΔCDM
b: ΔABM=ΔCDM
nên AB=CD và góc ABM=góc CDM
=>AB//CD
=>CE vuông góc với AC
=>AC vuông góc DE

a: Xét ΔADM và ΔCBM có
MA=MC
\(\widehat{AMD}=\widehat{CMB}\)
MD=MB
Do đó: ΔADM=ΔCBM
b: Xét tứ giác ABCD có
M là trung điểm của AC
M là trung điểm của BD
Do đó: ABCD là hình bình hành
Suy ra: AB//CD
hay CD\(\perp\)AC

a: Xét tứ giác ABDC có
M là trung điểm của AD
M là trung điểm của BC
Do đó: ABDC là hình bình hành
Suy ra: AB//CD

a: Xét ΔABM và ΔDCM có
MA=MD
\(\widehat{AMB}=\widehat{DMC}\)
MB=MC
Do đó: ΔABM=ΔDCM
nếu anh làm được bài này thi em có yêu anh ko
thế này đúng ko
a) Chứng minh : 𝛥ABM = 𝛥CDM
Xét 𝛥ABM và 𝛥CDM :
MA = MC (gt)
MB = MD (gt)
=> 𝛥ABM = 𝛥CDM (c – g – c)
b) Chứng minh : AB // CD
Ta có :
Mà :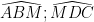 ở vị trí so le trong
ở vị trí so le trong
Nên : AB // CD
c) Chứng minh BK = DH
Xét 𝛥ABH và 𝛥CDK, ta có :
AB = CD (𝛥ABM = 𝛥CDM)
=> 𝛥ABH = 𝛥CDK (cạnh huyền – góc nhọn)
=> BH = CK (cạnh tương ứng)