Cho tam giác DEF nhọn nội tiếp đường tròn tâm (O). Vẽ DI vuông góc với EF, IK vuông góc với DE, IH vuông góc với DF
a) c/m DKIH nội tiếp đường tròn và xác định tâm của đường tròn đó
b) C/m \(\widehat{DHK}=\widehat{DEI}\)
ai tiếp mình nhja
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
2 tháng 4 2021
a) Xét tứ giác DFEC có
\(\widehat{DFC}=\widehat{DEC}\left(=90^0\right)\)
\(\widehat{DFC}\) và \(\widehat{DEC}\) là hai góc cùng nhìn cạnh DE
Do đó: DFEC là tứ giác nội tiếp(Dấu hiệu nhận biết tứ giác nội tiếp)
24 tháng 5 2023
c: AHIK nội tiếp
=>góc AIK=góc AHK
BHKC nội tiếp nên góc ICK=góc AHK
=>góc ICK=góc AIK
=>góc AIC=90 độ
AT
16 tháng 7 2021
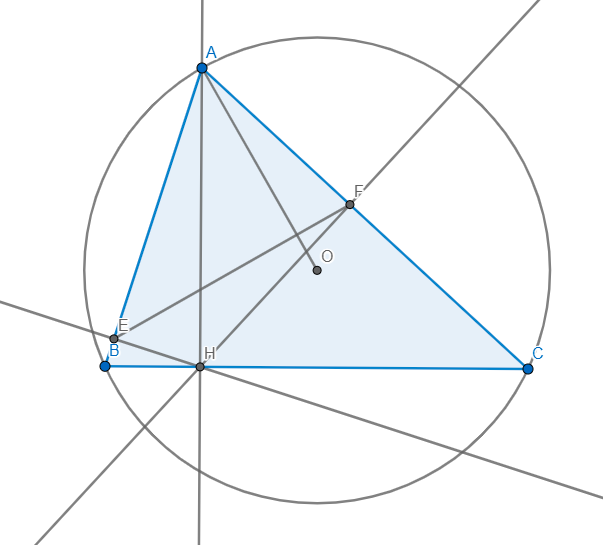
a) Ta có: \(\angle AEH+\angle AFH=90+90=180\Rightarrow AEHF\) nội tiếp
b) AEHF nội tiếp \(\Rightarrow\angle EFA=\angle EHA=90-\angle BHE=\angle ABC\)
c) Ta có: \(\angle OAC=\dfrac{180-\angle AOC}{2}=90-\dfrac{1}{2}\angle AOC=90-\angle ABC\)
\(\Rightarrow\angle OAC+\angle ABC=90\Rightarrow\angle OAC+\angle AFE=90\Rightarrow OA\bot EF\)
Ok
Hình bạn tự vẽ
Câu a
Tứ giác DKIH có
Góc IKD+ Góc IHD = 90°+90°= 180°
=> Tứ gác DKIH nội tiếp
Gọi A là trung điểm DI
∆ IHD vuông có HA là trung tuyến
∆IKD vuông có KA là trung tuyến
=> HA=KA=IA=DA
=> I là tâm đường tròn
Câu b
Tứ giác DKIH nội tiếp
=> góc KHD = Góc DIK
Ta có góc EDI + góc DEI = 90°
Lại có Góc KHI+góc KHD = 90°
Mà góc KDI = Góc KHI (Tứ giác DKIH nội tiếp; cùng chắn cung KI)
=> Cái đề