Cho tam giác ABC có 3 góc nhọn,kẻ AH vuông góc với BC ,biết HB < HC .CMR :góc HAB < góc HAC
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
27 tháng 4 2020
ta có BAHˆ=AHCˆ=AHBˆ=90BAH^=AHC^=AHB^=90
BAHˆ=ACBˆBAH^=ACB^ ( cùng phụ HACˆHAC^)
HACˆ=ABCˆHAC^=ABC^( cùng phụ BAHˆBAH^)
27 tháng 4 2020
Giải:
Có: HB < HC
Mà HB là hình chiếu của AB lên BC
HC là hình chiếu của AC lên BC
=> AB < AC ( mối quan hệ đường xiên và hình chiếu )
=> ^C < ^B => ^C - ^B < 0 (1)
Vì \(\Delta\)ABH vuông tại B => ^B + ^HAB = 90 độ
\(\Delta\)ACH vuông tại C => ^C + ^HAC = 90 độ
=> ^HAB + ^B = ^C + ^HAC
=> ^HAB - ^HAC = ^C - ^B < 0 ( theo (1))
=> ^HAB < ^HAC.
A
24 tháng 3 2019
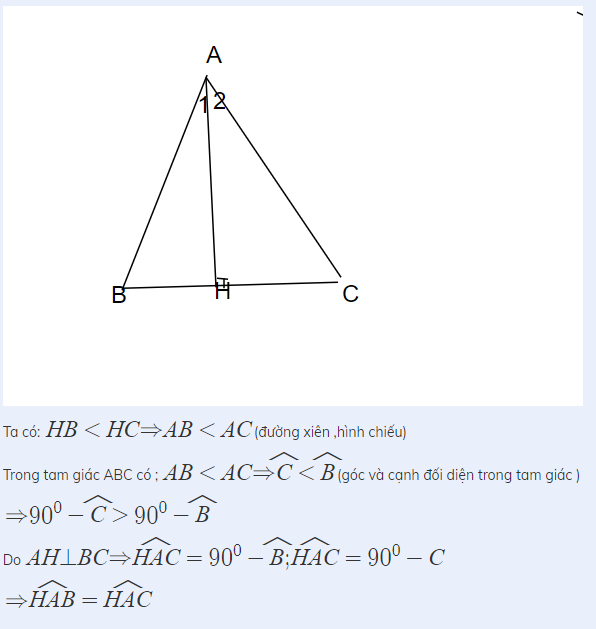
Ta có: \(HB< HC\Rightarrow AB< AC\)(đường xiên ,hình chiếu)
Trong tam giác ABC có ; \(AB< AC\Rightarrow\widehat{C}< \widehat{B}\)(góc và cạnh đối diện trong tam giác )
\(\Rightarrow90^0-\widehat{C}>90^0-\widehat{B}\)
Do \(AH\perp BC\Rightarrow\widehat{HAC}=90^0-\widehat{B};\widehat{HAC}=90^0-C\)
\(\Rightarrow\widehat{HAB}=\widehat{HAC}\)
24 tháng 3 2019
Trên HC lấy điểm E sao cho HB=HE.
Suy ra E nằm giữa H và C vì HE<HC.
Xét tam giác ABE có AE đồng thời là đường cao,đường trung tuyến nên tam giác ABE cân tại A.
\(\Rightarrow AB=AE,\widehat{ABE}=\widehat{AEB}\)
Do ^AEH là góc ngoài của tam giác AEC nên \(\widehat{AEH}>\widehat{ACB}\)
Suy ra \(\widehat{ABE}>\widehat{ACB}\)hay \(AB< AC\)(quan hệ giữa góc và cạnh đối diện)
Đến đây mới áp dụng như bạn được nhé.Đề đã cho AB<AC đâu!
PT
Cho tam giác ABC có ba góc nhọn, AB < AC. Kẻ AH vuông góc với BC tại H. So sánh H A B ^ và H A C ^ .
2
14 tháng 6 2017
Câu 1:
Xét tam giác ABH vuông tại H, ta có:
AB2 = AH2 + HB2 (định lý Py-ta-go)
202 = AH2 + 162
400 = AH2 + 256
AH2 = 400 - 256
AH2 = 144
AH = \(\sqrt{144}\)= 12 (cm)
Xét tam giác AHC vuông tại H, ta có:
AC2 = AH2 + HC2 (định lý Py-ta-go)
AC2 = 122 + 52
AC2 = 144 + 25
AC2 = 169
AC = \(\sqrt{169}\)= 13 (cm)
Vậy AH = 12 cm
AC = 13 cm
Bài 2:
Xét tam giác AHC vuông tại H, ta có:
AC2 = AH2 + HC2 (định lý Py-ta-go)
152 = AH2 + 92
225 = AH2 + 81
AH2 = 225 - 81
AH2 = 144
AH = \(\sqrt{144}\)= 12 (cm)
Xét tam giác AHB vuông tại, ta có:
AB2 = AH2 + HB2 (định lý Py-ta-go)
AB2 = 122 + 52
AB2 = 144 + 25
AB2 = 169
AB = \(\sqrt{169}\)= 13 (cm)
Vậy AB = 13 cm
29 tháng 7 2023
a: Xét ΔABC có AC>AB
nên góc B>góc C
b: Xét ΔABC có AB<AC
mà HB,HC lần lượt là hình chiếu của AB,AC trên BC
nên HB<HC
c: góc B+góc C=90 độ
góc HAC+góc C=90 độ
=>góc B=góc HAC
góc C+góc B=90 độ
góc HAB+góc B=90 độ
=>góc C=góc HAB
YT
1
31 tháng 1
Ta có: \(\widehat{HAB}+\widehat{B}=90^0\)(ΔHAB vuông tại H)
\(\widehat{HAC}+\widehat{C}=90^0\)(ΔHAC vuông tại H)
mà \(\widehat{HAB}< \widehat{HAC}\)
nên \(\widehat{B}>\widehat{C}\)
Xét ΔABC có \(\widehat{B}>\widehat{C}\)
mà AC,AB lần lượt là cạnh đối diện của các góc ABC và góc ACB
nên AC>AB
Xét ΔABC có
AB<AC
HB,HC lần lượt là hình chiếu của AB,AC trên BC
Do đó: HB<HC