Một đường tròn và một tam giác được vẽ trên cùng mặt phẳng. Hỏi có nhiều nhất bao nhiêu miền được tạo ra trên mặt phẳng?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


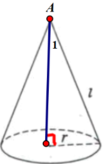
Cắt mặt xung quanh của một hình nón tròn xoay dọc theo một đường sinh rồi trải ra trên mặt phẳng ta được một nửa hình tròn bán kính R ⇒ đường sinh có độ dài bằng R và chu vi đường tròn đáy bằng nửa chu vi đường tròn bán kính R
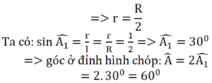

Vẽ hình:
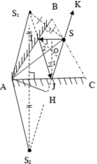
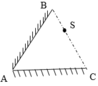
a) S1 là ảnh của S qua gương AB => S1 đối xứng với S qua AB
S2 là ảnh của S1 qua gương AC => S2 đối xứng với S 1 qua AC
Ta nối S2 với S cắt AC tại J, nối J với S1 cắt AB tại I
=> SI, IJ, JS là ba đoạn của tia sáng cần dựng.
b) Dựng hai phỏp tuyến tại I và J cắt nhau tai O
Góc tạo bởi tia phản xạ JK và tia tới SI là ∠ ISK
Theo tính chất góc ngoài tam giác ta có
I S K ^ = I ^ + J ^ = 2 I ^ 2 + 2 J ^ 2 = 2 ( 180 0 − I O ^ J ) = 2. B A ^ C = 120 0
c) Tổng độ dài ba đoạn:
SI + IJ + JS = S1I + IJ + JS = S1J + JS = S2J + JS = S2S
(Đối xứng trục)
Vậy SI + IJ + JS = S2S
Ta có:
∠ S1AS = 2 ∠ S1AB (1)
∠ S1AS2 = 2 ∠ S1AC (2)
Lấy (2) – (1):
∠ S1AS2 - ∠ S1AS = 2( ∠ S1AC - ∠ S1AB)
ð ∠ SAS2 = 2 ∠ BAC
ð ∠ SAS2 = 1200
Xét tam giác cân SAS2 tại A, có ∠ A = 1200
ð ∠ ASH = ∠ AS2H = 300 với đường cao AH, ta có: SS2 = 2SH
Xét tam giác vuông SAH taị H có ∠ ASH = 300 ta có: AH = AS/2
Trong tam giác vuông SAH tại H.
Theo định lí pitago ta tính được SH= S A . 3 2
nên SS2 = 2SH = 2. S A . 3 2 = SA 3
=> SS2 nhỏ nhất ó SA nhỏ nhất ó AS là đường cao của tam giác đều ABC
ó S là trung điểm của BC.
mấy dòng cúi đọc chả hiểu j nhưng mình vẫn chép
thank you so much
I LOVE YOU chụt chụt...

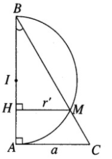
Tam giác vuông ABC có BC = 2a và AC = a nên ta suy ra ∠ ABC = 30 ° . Khi quay xung quanh trục AB cạnh BC tạo nên mặt nón tròn xoay có góc ở đỉnh bằng 60 ° và có đường tròn đáy có bán kính AC = a. Khi xoay xung quanh trục AB nửa đường tròn đường kính AB tạo nên mặt cầu có tâm là trung điểm I để đoạn AB và bán kính r = AB/2.
kick cho minh di minh ko biet