tìm nghiệm nguyên của phương trình
4x + 5y = 21
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NT
1
26 tháng 3 2018
Ta có : 4x + 5y = 21
<=> 4x = 21 - 5y
<=> x = \(\frac{21-5y}{4}\)
Để x nguyên thì : \(\frac{21-5y}{4}\) nguyên
<=> 21 - 5y thuộc B(4) = {0;4;8;12;......}
<=> 5y thuộc {21;18;14;10;......}
<=> y = 5
Vậy y = 5 => 4x = 21 - 5.5 = -4 => x = -1
CN
2
6 tháng 2 2018
\(PT\Leftrightarrow\left(x^2-4xy+4y^2\right)+4x-8y+4+y^2-16=0\)
\(\Leftrightarrow\left(x-2y\right)^2+4\left(x-2y\right)+4+y^2=16\)
\(\Leftrightarrow\left(x-2y+2\right)^2+y^2=16\)
Vì \(\left(x+2y+2\right)^2+y^2\) là tổng hai số chính phương
nên \(\left(\left(x+2y+2\right)^2;y^2\right)\in\left\{0;16\right\}\)xét 2 TH là ra
3 tháng 10 2021
Bài 1:
3x+2y=7
\(\Leftrightarrow3x=7-2y\)
\(\Leftrightarrow x=\dfrac{7-2y}{3}\)
Vậy: \(\left\{{}\begin{matrix}y\in R\\x=\dfrac{7-2y}{3}\end{matrix}\right.\)
OM
0
9 tháng 3 2018
Tìm nghiệm nguyên của các phương trình sau:
a) 12x - 7y = 45 (1)
ta thấy 45 và 12 chia hết cho 3 nên y cũng phải chia hết cho 3
đặt y=3k, ta có:
12x-7.3k=45
<=> 4x-7k=15 (chia cả 2 vế cho 3)
<=> x= \(\frac{15+7k}{4}\)
<=> x= \(2k+4-\frac{k+1}{4}\)
đặt t=\(\frac{k+1}{4}\)(t \(\in\) Z) => k = 4t – 1
Do đó
x = 2(4t – 1) + 4 – t = 7t + 2
y = 3k = 3(4t - 1) = 12t – 3
Vậy nghiệm nguyên của phương trình được biểu thị bởi công thức:
\(\hept{\begin{cases}x=7t+2\\y=12t-3\end{cases}}\)
Câu b và c bạn làm tương tự
Thấy đúng thì k cho mình nhé
4 tháng 10 2021
\(1,3x+2y=7\\ \Leftrightarrow2y=7-3x\left(1\right)\)
Vì \(2y⋮2\)
\(\Leftrightarrow3x-7⋮2\\ \Leftrightarrow3x-9⋮2\\ \Leftrightarrow3\left(x-3\right)⋮2\\ \Leftrightarrow x-3⋮2\\ \Leftrightarrow x.lẻ\)
Đặt \(x=2k+1\left(k\in Z\right)\)
Thay vào (1), ta được :
\(\left(1\right)\Leftrightarrow2y=3\left(2k+1\right)-7\\ \Leftrightarrow2y=6k+3-7\\ \Leftrightarrow2y=6k-4\\ \Leftrightarrow y=3k-2\)
Vậy \(x=2k+1;y=3k-2\left(k\in Z\right)\)
\(2,C_1:\left\{{}\begin{matrix}-2x+y=1\\4x+5y=3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}-4x+2y=2\\4x+5y=3\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}4x+5y=2\\7y=5\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=-\dfrac{1}{7}\\y=\dfrac{5}{7}\end{matrix}\right.\\ C_2:\left\{{}\begin{matrix}-2x+y=1\\4x+5y=3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=1+2x\\4x+5y=3\end{matrix}\right.\Leftrightarrow4x+5+10x=3\\ \Leftrightarrow x=-\dfrac{1}{7}\Leftrightarrow y=1-\dfrac{2}{7}=\dfrac{5}{7}\)
C
0
CM
6 tháng 9 2019
a) 3x – y = 2 (1)
⇔ y = 3x – 2.
Vậy phương trình có nghiệm tổng quát là (x; 3x – 2) (x ∈ R).
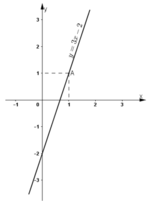
Đường thẳng biểu diễn tập nghiệm của phương trình (1) là đường thẳng y = 3x – 2 (Hình vẽ).
+ Tại x = 2/3 thì y = 0 ⇒ đường thẳng y = 3x – 2 đi qua điểm (2/3 ; 0).
+ Tại x = 0 thì y = -2 ⇒ đường thẳng y = 3x – 2 đi qua điểm (0; -2).
Vậy đường thẳng y = 3x – 2 là đường thẳng đi qua điểm (2/3 ; 0) và (0; -2).
b) x + 5y = 3 (2)
⇔ x = 3 – 5y
Vậy phương trình có nghiệm tổng quát là (3 – 5y; y) (y ∈ R).
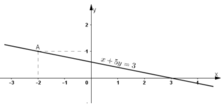
Đường thẳng biểu diễn tập nghiệm của (2) là đường thẳng x + 5y = 3.
+ Tại y = 0 thì x = 3 ⇒ Đường thẳng đi qua điểm (3; 0).
+ Tại x = 0 thì y=3/5 ⇒ Đường thẳng đi qua điểm (0; 3/5).
Vậy đường thẳng x + 5y = 3 là đường thẳng đi qua hai điểm (3; 0) và (0; 3/5).
c) 4x – 3y = -1
⇔ 3y = 4x + 1
⇔ 
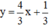
Vậy phương trình có nghiệm tổng quát là (x;4/3x+1/3)(x ∈ R).
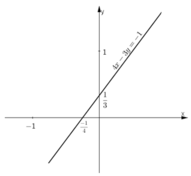
Đường thẳng biểu diễn tập nghiệm phương trình là đường thẳng 4x – 3y = -1.
+ Tại x = 0 thì y = 1/3
Đường thẳng đi qua điểm (0;1/3) .
+ Tại y = 0 thì x = -1/4
Đường thẳng đi qua điểm (-1/4;0) .
Vậy đường thẳng 4x – 3y = -1 đi qua (0;1/3) và (-1/4;0).
d) x + 5y = 0
⇔ x = -5y.
Vậy nghiệm tổng quát của phương trình là (-5y; y) (y ∈ R).
Đường thẳng biểu diễn nghiệm của phương trình là đường thẳng x + 5y = 0.
+ Tại x = 0 thì y = 0 ⇒ Đường thẳng đi qua gốc tọa độ.
+ Tại x = 5 thì y = -1 ⇒ Đường thẳng đi qua điểm (5; -1).
Vậy đường thẳng x + 5y = 0 đi qua gốc tọa độ và điểm (5; -1).
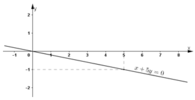
e) 4x + 0y = -2
⇔ 4x = -2 ⇔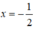 
Phương trình có nghiệm tổng quát (-0,5; y)(y ∈ R).
Đường thẳng biểu diễn tập nghiệm là đường thẳng x = -0,5 đi qua điểm (-0,5; 0) và song song với trục tung.
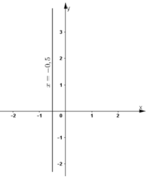
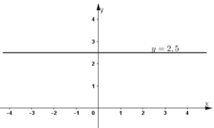
f) 0x + 2y = 5
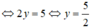
Phương trình có nghiệm tổng quát (x; 2,5) (x ∈ R).
Đường thẳng biểu diễn tập nghiệm là đường thẳng y = 2,5 đi qua điểm (0; 2,5) và song song với trục hoành.
\(x=\frac{21-5y}{4}=\frac{20-4y+1-y}{4}=5-y+\frac{1-y}{4}\)
=> Để x nguyên thì 1-y = 4k (k thuộc Z) => y=1-4k
x=5-1+4k+k = 5k+4
Vậy các cặp (x,y) thuộc Z thỏa mãn là (5k+4; 1-4k) với k thuộc Z
mk nháp được 2 kết quả x=4+5k y=1-4k
x=4-5k y=4k+1