Giúp em câu 2c và ạ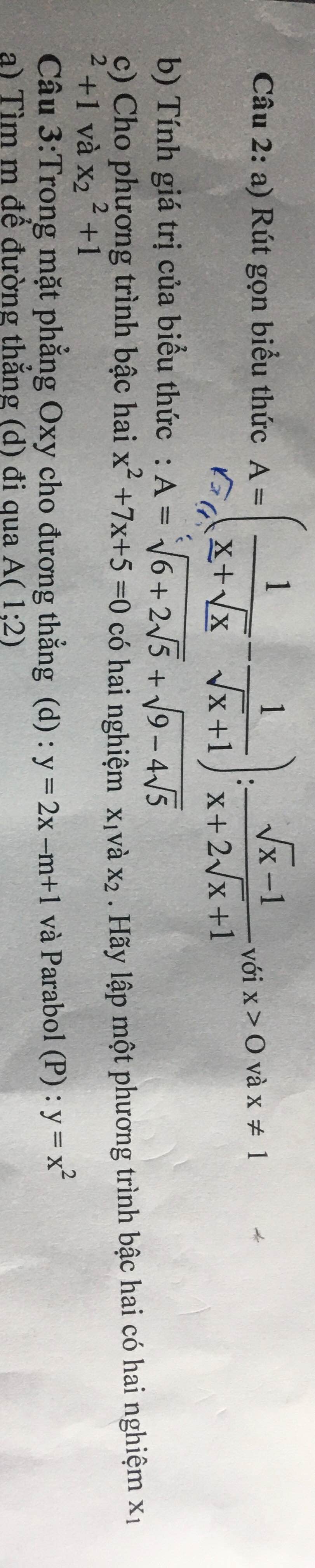 
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
31 tháng 8 2021
Đk:
x^2 - 9 ≠ 0
=> x ≠ 3 (1)
5 - x ≥ 0
=> x ≤ 5 (2)
x + 2 ≥ 0
=> x ≥ -2 (3)
(1),(2),(3) => -2 ≤ x ≠ 3 ≤ 5
31 tháng 8 2021
Bài 3:
a: Để hàm số (*) là hàm số bậc nhất thì \(m-2\ne0\)
hay \(m\ne2\)
b: Để hàm số (*) đồng biến trên R thì m-2>0
hay m>2
c: Thay x=-2 và y=3 vào (*), ta được:
\(-2\left(m-2\right)+2m-1=3\)
\(\Leftrightarrow-2m+4+2m-1=3\)(luôn đúng)
NT
2
6 tháng 5 2022
2.c
\(x+\sqrt{4x^2-4x+1}=5\)
\(\Leftrightarrow x+\sqrt{\left(2x-1\right)^2}=5\)
\(\Leftrightarrow x+\left|2x-1\right|=5\)
\(\Leftrightarrow\left[{}\begin{matrix}x+2x-1=5;x\ge\dfrac{1}{2}\\x+1-2x=5;x< \dfrac{1}{2}\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}3x=6\\-x=4\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}x=2\left(tm\right)\\x=-4\left(tm\right)\end{matrix}\right.\)
Vậy \(S=\left\{2;-4\right\}\)
HK
2
23 tháng 4 2022
1)sao phân biệt được v của ai A hay B sửa vA và vB
a)thời gian của hai xe gặp nhau
t=sAB/vA+vB=2/9h=800s
b)sau 0,5h thì người đi từ A đi được
sA=vA.tA=30km
sau 0,5h thì người đi từ B đi được
sB=vB.tB=15km
khoảng cách của hai xe lúc này
s1=(sA+sB)-sAB=25km
c)sau 1h thì người đi từ A đi được
sA1=vA.tA1=60km
sau 1h thì người đi từ B đi được
sB1=vB.tB1=30km
khoảng cách của hai xe lúc này
s2=(sA+sB)-sAB=70km
d)tổng quãng đường đi được ;20-10=10km
sA+sB=10
vA.tA2+vB.tB2=10
60.t+30.t=10
90t=10
t=1/9h
23 tháng 4 2022
câu 2,3 giống cách làm nhưng đáp án khác dựa vào đó làm dễ mà
4 tháng 6 2021
\(\dfrac{1}{c}+b^2c=ab\left(a+b+c\right)+b^2c=ab\left(a+c\right)+b^2\left(a+c\right)=b\left(a+b\right)\left(a+c\right)\)
\(\dfrac{1}{c}+a^2c=ab\left(a+b+c\right)+a^2c=a\left(a+b\right)\left(b+c\right)\)
\(\Rightarrow\left(\dfrac{1}{c}+b^2c\right)\left(\dfrac{1}{c}+a^2c\right)=ab\left(a+b\right)^2\left(b+c\right)\left(a+c\right)\)
\(\Leftrightarrow\left(1+b^2c^2\right)\left(1+a^2c^2\right)=c^2\left(a+b\right)^2ab\left(ab+bc+ac+c^2\right)\)\(=c^2\left(a+b\right)^2\left(a^2b^2+ab^2c+a^2bc+abc^2\right)\)\(=c^2\left(a+b\right)^2\left[a^2b^2+abc\left(a+b+c\right)\right]=c^2\left(a+b\right)^2\left(a^2b^2+1\right)\)
\(\Rightarrow\dfrac{\left(1+b^2c^2\right)\left(1+a^2c^2\right)}{c^2\left(a^2b^2+1\right)}=\left(a+b\right)^2\)
\(\Leftrightarrow\sqrt{\dfrac{\left(1+b^2c^2\right)\left(1+a^2c^2\right)}{c^2+a^2b^2c^2}}=a+b\) (đpcm)
25 tháng 12 2023
Bài 3:
2:
a: Thay m=0 vào (d), ta được:
\(y=\left(0+1\right)x-2=x-2\)
b: Thay x=1 vào y=x+1, ta được:
y=1+1=2
Thay x=1 và y=2 vào (d), ta được:
1(m+1)-2=2
=>m+1=4
=>m=3
c: Để \(\widehat{OAB}=45^0\) thì góc tạo bởi (d) với trục Ox bằng 45 độ
(d): y=(m+1)x-2
=>a=m+1
\(\Leftrightarrow tanOAB=a=m+1\)
=>m+1=tan45=1
=>m=0
Theo viet có:\(\left\{{}\begin{matrix}x_1+x_2=-7\\x_1x_2=5\end{matrix}\right.\)
Có \(x_1^2+1+x_2^2+1=\left(x_1+x_2\right)^2-2x_1x_2+2=\left(-7\right)^2-2.5+2=41\)
\(\left(x_1^2+1\right)\left(x_2^2+1\right)=x_1^2x_2^2+x_1^2+x_2^2+1=5^2+40=65\)
\(\Rightarrow\left(x_1^2+1\right);\left(x_2^2+1\right)\) là nghiệm của pt: \(t^2-41t+65=0\)