Cho AB=10cm.Tính A'B',A"B"
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
18 tháng 9 2016
a) Ta có \(O_2=O_3\) ( Om p/g )
xOy = yOm ( Om p/g )
→ \(xOy-O_2=yOm-O_3\)
→ \(O_1=O_4\)
b) + Xét Δ ABO và Δ AB'O có : \(O_1=O_4\left(cmt\right)\)
\(\begin{cases}OA=OA'\\OB=OB'\end{cases}\left(gt\right)\)
Nên Δ ABO = Δ AB'O ( cgc ) → AB = AB'
Xét Δ AB'O = Δ A'BO có : xOt = zOy ( vì \(O_1=O_4\) )
\(\begin{cases}OA=OA'\\OB=OB'\end{cases}\left(gt\right)}\)
→ \(O_1+zOt=O_4+xOt\Rightarrow O_4+zOt\Rightarrow xOt=zOy\)
Nên Δ AB'O = Δ A'BO ( cgc ) → AB' = A'B
c) Ta có : OA =OA' ( gt ) → Δ OAA' cân tại O → góc OAA' = góc OA'A
Mà có : góc OAB' = góc OA'B → góc OAA' - góc OAB' = góc OA'A = góc OA'B
→ góc B'AA' = góc BA'A → Δ AIA' cân tại I → IA = IA'
Mà A'B = AB' → A'B - A'I = AB' - AI
→ IB = IB'
d) Xét Δ OBI và Δ OB'I có : OI chung
IB = IB' ( C/m c )
OB = OB' ( gt )
Nên Δ OBI = Δ OB'I ( ccc ) → góc BOI = B'OI
Mà OI nằm giữa Oz và Ot → OI là p/g góc zOt. Mà có Om cũng là p/g góc zOt .
→ \(I\in Om\) hay AB', A'B và Om đồng qui
CM
29 tháng 5 2017
Ta có
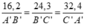
a) Tính được A'B' = 6,2cm. Từ đó tính được B'C' = 9,3cm và A'C' = 12,4cm.
b) Tương tự câu a tính được A'B' = 26,2cm, B'C' = 39,3cm và A'C' = 52,4cm
12 tháng 3 2020
a) \(\frac{AB+CD}{CD}=\frac{AB}{CD}+1\)Hay \(\frac{AB+CD}{CD}=\frac{4}{5}+1=\frac{9}{5}\)
b) \(\frac{C'D'-A'B'}{A'B'}=\frac{C'D'}{A'B'}-1\)Hay \(\frac{C'D'-A'B'}{A'B'}=\frac{5}{4}-1=\frac{1}{4}\)
=> \(\frac{A'B'}{C'D'-A'B'}=4\)
c) Ta có: 3CD = C'D' => \(\frac{CD}{C'D'}=\frac{1}{3}\)
Mà \(\frac{CD}{C'D'}=\frac{AB}{A'B'}\) nên \(\frac{AB}{A'B'}=\frac{1}{3}\)
CM
24 tháng 5 2017
Ta có: AB/A'B' = CD/C'D' ⇒ AB.C'D' = A'B'.CD ⇔ AB/CD = A'B'/C'D'
Khi đó cả ( I ),( II ) đều đúng.
Chọn đáp án B.