Cho đường thẳng xy,trên đó lấy A sao cho góc xAz = 800.Tính góc zAy
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Ta có: `hat(xAz)+hat(zAy)=180^@`
Mà `hat(xAz)=5.hat(zAy)` (GT)
`=>5.hat(zAy)+hat(zAy)=180^@`
`=>6.hat(zAy)=180^@`
`=>hat(zAy)=180^@ : 6=30^@`
``
+) `hat(xAz)=5.hat(zAy)=5.30^@=150^@`
+) `hat(xAt)` và `hat(zAy)` đối đỉnh `=> hat(xAt)=hat(zAy)=30^@`

a) A B I M
IA + IB = (IB+ AB) + IB = 2. IB + AB= 2. IB + 2. MB = 2.(IB + MB) = 2. IM = 2.a
b) A x y z t
yAz = 1/2 yAt => yAt = 2. yAz
góc xAz = 180o - yAz
góc xAt = 180o - yAt
mà góc xAz = 3.góc xAt => 180o - yAz = 3. (180o - yAt ) => 180o - yAz = 3. (180o - 2.yAz )
=> 180o - yAz = 540o - 6.yAz => 6. yAz - yAz = 540 - 180 => 5.yAz = 360 => góc yAz = 360 : 5 = 72o
=> góc xAz = 180 - 72 = 108 độ
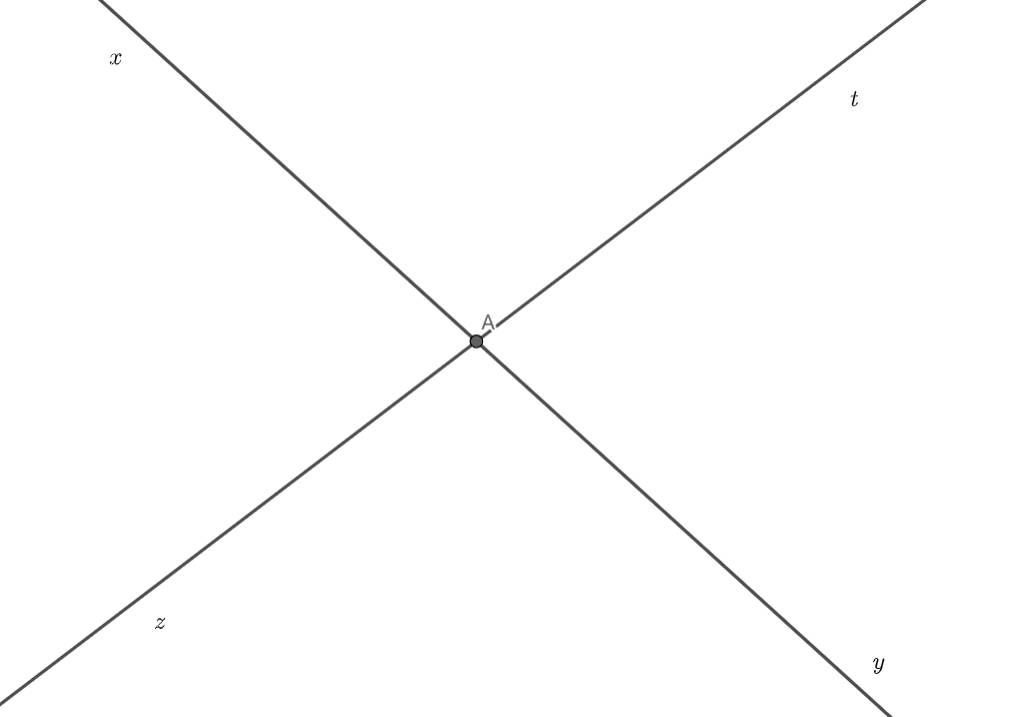

Ta có:
Góc xAy là góc bẹt
\(\Rightarrow\widehat{xAy}=180^o\)
Trên nửa mặt phẳng bờ chứa tia Ax có \(\widehat{xAz}\)= 80o , \(\widehat{xAy}=180^o\); mà 80o < 180o \(\Rightarrow\widehat{xAz}< \widehat{xAy}\)\(\Rightarrow\)Tia Az nằm giữa hai tia Ax và Ay
\(\Rightarrow\widehat{xAz}+\widehat{zAy}=\widehat{xAy}\)
\(\Rightarrow80^o+\widehat{zAy}=180^o\)
\(\Rightarrow\widehat{zAy}=180^o-80^o=100^o\)
Vậy \(\widehat{zAy}=100^o\)
. x y z A
Vì điểm A nằm trên đường thẳng xy
=> \(\widehat{xAy}\) là góc bẹt
=> Tia Az nằm giữa hai tia Ax và Ay
=> \(\widehat{xAz}+\widehat{zAy}=\widehat{xAy}\)
Thay \(\widehat{xAz}=80^o,\widehat{xAy}=180^o\), ta có:
\(80^o+\widehat{zAy}=180^o\)
=> \(\widehat{zAy}=180^o-80^o\)
=> \(\widehat{zAy}=100^o\)
Vậy \(\widehat{zAy}=100^o\)