. Cho ba số dương 0=<a=<b=<c chứng minh rằng:\(\frac{a}{bc+1}+\frac{b}{ac+1}+\frac{c}{ab+1}\)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


nhanh lên các bạn ơi .ngày kia mình cần rồi .ai làm vừa ý mình mình link cho

Làm vô đây đài nhưng làm trog giấy ngắn lắm
1) a # b # c # a, thỏa a/(b-c) + b/(c-a) + c/(a-b) = 0
<=> a(c-a)(a-b) + b(a-b)(b-c) + c(b-c)(c-a) = 0
<=> -a(a-b)(a-c) - b(b-a)(b-c) - c(c-a)(c-b) = 0
<=> a(a-b)(a-c) + b(b-a)(b-c) + c(c-a)(c-b) = 0 (*)
từ (*) ta thấy a, b, c đối xứng nên không giãm tính tổng quát giả sử: a > b > c
* Nếu a, b, c đều không âm, giả thiết trên thành a > b > c ≥ 0
(*) <=> (a-b)(a² - ac - b² + bc) + c(c-a)(c-b) = 0
<=> (a-b)[(a+b)(a-b) -c(a-b)] + c(c-a)(c-b) = 0
<=> (a-b)².(a+b-c) + c(a-c)(b-c) = 0 (1*)
thấy b - c > 0 (do b > c) và a > 0 => a+b-c > 0 => (a-b)².(a+b-c) > 0 và c(a-c)(b-c) ≥ 0
=> (a-b)².(a+b-c) + c(a-c)(b-c) > 0 mâu thuẩn với (1*)
Vậy c < 0 (nói chung là trong a, b, c phải có số âm)
* Nếu cả a, b, c đều không có số dương do giả thiết trên ta có: 0 ≥ a > b > c
(*) <=> a(a-b)(a-c) + (b-c)(b² - ab - c² + ca) = 0
<=> a(a-b)(a-c) + (b-c)[(b+c)(b-c) - a(b-c)] = 0
<=> a(a-b)(a-c) + (b-c)².(b+c-a) = 0 (2*)
a - b > 0; a - c > 0 => a(a-b)(a-c) ≤ 0 (vì a ≤ 0)
và b < 0; c - a < 0 => b + c -a < 0 => (b-c)².(b+c-a) < 0
=> a(a-b)(a-c) + (b-c)².(b+c-a) < 0 mẫu thuẩn với (2*)
chứng tỏ trong a, b, c phải có số dương
Tóm lại trong 3 số a, b, c phải có số dương và số âm
1) a # b # c # a, thỏa a/(b-c) + b/(c-a) + c/(a-b) = 0
<=> a(c-a)(a-b) + b(a-b)(b-c) + c(b-c)(c-a) = 0
<=> -a(a-b)(a-c) - b(b-a)(b-c) - c(c-a)(c-b) = 0
<=> a(a-b)(a-c) + b(b-a)(b-c) + c(c-a)(c-b) = 0 (*)
từ (*) ta thấy a, b, c đối xứng nên không giãm tính tổng quát giả sử: a > b > c
* Nếu a, b, c đều không âm, giả thiết trên thành a > b > c ≥ 0
(*) <=> (a-b)(a² - ac - b² + bc) + c(c-a)(c-b) = 0
<=> (a-b)[(a+b)(a-b) -c(a-b)] + c(c-a)(c-b) = 0
<=> (a-b)².(a+b-c) + c(a-c)(b-c) = 0 (1*)
thấy b - c > 0 (do b > c) và a > 0 => a+b-c > 0 => (a-b)².(a+b-c) > 0 và c(a-c)(b-c) ≥ 0
=> (a-b)².(a+b-c) + c(a-c)(b-c) > 0 mâu thuẩn với (1*)
Vậy c < 0 (nói chung là trong a, b, c phải có số âm)
* Nếu cả a, b, c đều không có số dương do giả thiết trên ta có: 0 ≥ a > b > c
(*) <=> a(a-b)(a-c) + (b-c)(b² - ab - c² + ca) = 0
<=> a(a-b)(a-c) + (b-c)[(b+c)(b-c) - a(b-c)] = 0
<=> a(a-b)(a-c) + (b-c)².(b+c-a) = 0 (2*)
a - b > 0; a - c > 0 => a(a-b)(a-c) ≤ 0 (vì a ≤ 0)
và b < 0; c - a < 0 => b + c -a < 0 => (b-c)².(b+c-a) < 0
=> a(a-b)(a-c) + (b-c)².(b+c-a) < 0 mẫu thuẩn với (2*)
chứng tỏ trong a, b, c phải có số dương
Tóm lại trong 3 số a, b, c phải có số dương và số âm
Tk mk nha

Ta có:

Dấu “=” xảy ra khi và chỉ khi


Vậy số bộ a,b,c thỏa mãn điều kiện đã cho là 1.
Chọn B.

a)
giải thích:
b) a nguyên dương, nguyên âm thì tích ab là số nguyên âm.
c) b = 0 thì tích ab bằng 0.

ê cu vô cái link này nè http://olm.vn/hoi-dap/question/94896.html tui vừa chép xong
ooooooooooooooooooooooooooooooooooooooooooooooo
oooooooooooooooooooooooooooooooooooooooooooooo
ooooooooooooooooooooooooooooooooooooooooooooooooo
ooooooooooooooooooooooooooooooooooooooooooooooooooo
ooooooooooooooooooooooooooooooooooooooooooooooooooooooooooo
ooooooooooooooooooooooooooooooooooooooooooooooooooo
cho ba số dương \(0\le a\le b\le c\le1\) CMR \(\dfrac{a}{bc+1}+\dfrac{b}{ac+1}+\dfrac{c}{ab+1}\le2\)

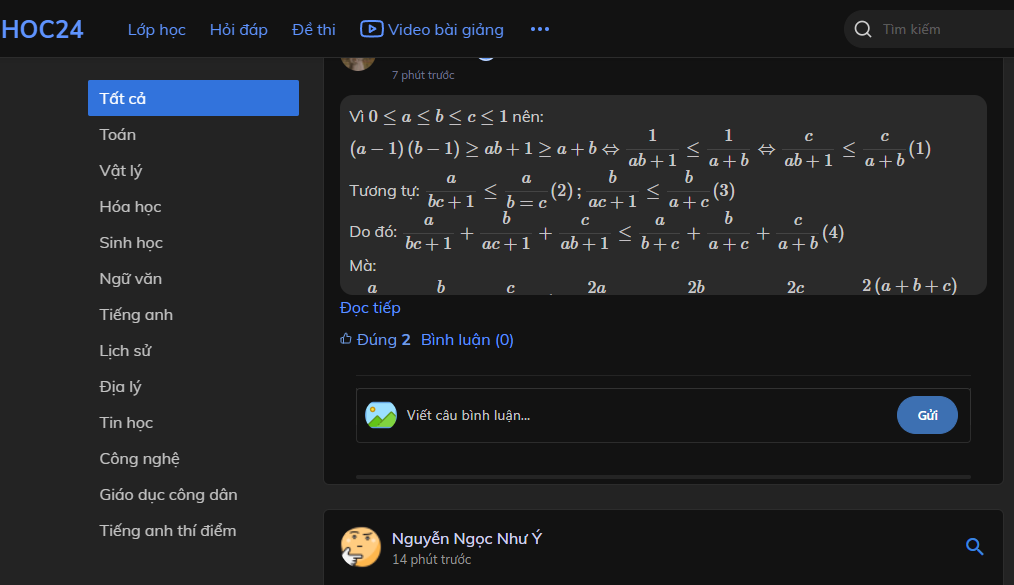
Vì \(0\le a\le b\le c\le1\) nên:
\(\left(a-1\right)\left(b-1\right)\ge ab+1\ge a+b\Leftrightarrow\dfrac{1}{ab+1}\le\dfrac{1}{a+b}\Leftrightarrow\dfrac{c}{ab+1}\le\dfrac{c}{a+b}\left(1\right)\)
Tương tự: \(\dfrac{a}{bc+1}\le\dfrac{a}{b=c}\left(2\right);\dfrac{b}{ac+1}\le\dfrac{b}{a+c}\left(3\right)\)
Do đó: \(\dfrac{a}{bc+1}+\dfrac{b}{ac+1}+\dfrac{c}{ab+1}\le\dfrac{a}{b+c}+\dfrac{b}{a+c}+\dfrac{c}{a+b}\left(4\right)\)
Mà: \(\dfrac{a}{b+c}+\dfrac{b}{a+c}+\dfrac{c}{a+b}\le\dfrac{2a}{a+b+c}+\dfrac{2b}{a+b+c}+\dfrac{2c}{a+b+c}=\dfrac{2\left(a+b+c\right)}{a+b+c}=2\left(5\right)\)
Từ (4) và (5) suy ra \(\dfrac{a}{bc+1}+\dfrac{b}{ac+1}+\dfrac{c}{ab+1}\left(đpcm\right)\)

Ta có: \(0\le a\le b\le c\le1\Leftrightarrow\left(1-a\right)\left(1-b\right)\ge0\)
\(\Rightarrow1-b-a+ab\ge0\Leftrightarrow1+ab\ge a+b\)
Tiếp tục chứng minh.
\(\hept{\begin{cases}1\ge c\\0\le a\le b\Leftrightarrow ab\ge0\end{cases}}\)
Cộng theo vế: \(2\left(ab+1\right)\ge a+b+c\)
Trở lại bài toán: \(\frac{c}{ab+1}=\frac{2c}{2\left(ab+1\right)}\le\frac{2c}{a+b+c}\)
Tương tự rồi cộng theo vế suy ra đpcm
Ta có: \(a\le1\Rightarrow a-1\le0\)
\(b\le1\Rightarrow b-1\le0\)
Ta có: \(\left(a-1\right)\left(b-1\right)\ge0\)( mới chứng minh ở trên đó )
\(\Rightarrow ab-a-b+1\ge0\Leftrightarrow ab+1\ge a+b\Leftrightarrow2ab+1\ge ab\ge a+b\)
\(\Rightarrow2ab+2\ge a+b+c\Leftrightarrow\frac{1}{2}ab+2\ge\frac{1}{a+b+c}+\frac{c}{ab+1}\le\frac{2c}{a+b+c}\)
Ta cũng chứng minh tương tự với \(\frac{b}{ac+1}\le\frac{2b}{a+b+c};\frac{a}{bc+1}\le\frac{2a}{a+b+c}\)
Từ đây bạn tự làm tiếp rồi suy ra đpcm nha
xin lỗi biểu thức daì đó phải=<2