Chứng minh góc ngoài của tam giác bằng tổng hai góc trong không kề
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
14 tháng 3 2022
1.Khẳng định nào sau đây không đúng:
A. Góc ngoài của tam giác bằng tổng hai góc trong không kề với nó
B. Trong tam giác cân hai góc ở đáy bằng nhau
C. Tam giác có hai góc bằng nhau là tam giác đều
2.Tam giác nào là tam giác vuông với số đo 3 cạnh như sau:
A. 13m; 14m; 15m B. 11m; 12m; 10m
C. 12m; 9m; 15m D. 8m; 8m; 10m
D. Trong tam giác đều mỗi góc bằng 60 độ
2 tháng 10 2021
| GT | \(\Delta ABC\), Ax đối AC |
| KL | \(\widehat{xAB}=\widehat{ABC}+\widehat{ACB}\) |
MN
16 tháng 2 2022
Tham khảo :
* Chứng minh:
a)
Ta có:
Tổng ba góc của tam giác \(ABC\) bằng \(180^o\) nên \(\widehat A + \widehat B = {180^o} - \widehat C\)
Góc \(ACx\) là góc ngoài của tam giác \(ABC\) nên\(\widehat {ACx}= 180^o-\widehat C\)
Do đó: \(\widehat {ACx} = \widehat A + \widehat B\).
b) Tam giác \(ABC\) vuông tại \(A\)
\( \Rightarrow \widehat A = {90^o}\)
Áp dụng định lí tổng các góc của một tam giác vào\(\Delta ABC\) ta có:
\(\widehat A + \widehat B + \widehat C = {180^o}\)
\( \Rightarrow \widehat B + \widehat C = {180^o} - \widehat A = {180^o} - {90^o} = {90^o}\)
c) Giả sử có tam giác \(ABC\) đều
\( AB = AC =BC \)
\( ΔABC\) cân tại \(A\) và cân tại \( B\).
\( \Rightarrow \widehat A = \widehat B;\,\,\,\,\widehat A = \widehat C\) (tính chất tam giác cân)
\( \Rightarrow \widehat A = \widehat B = \widehat C\)
d) Giả sử\(\Delta ABC\) có\(\widehat A = \widehat B = \widehat C\)
Có\(\widehat A = \widehat B\Rightarrow \)\(\Delta ABC\) cân tại \(C\), do đó \(CA=CB\).
Có\(\widehat B = \widehat C\Rightarrow \) \(\Delta ABC\) cân tại \(A\) do đó \(AC=AB\)
\( AB = AC = BC ΔABC\) là tam giác đều.
CM
13 tháng 4 2017
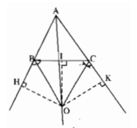
Giả sử hai tia phân giác của các góc ngoài tại đỉnh B và C của tam giác ABC cắt nhau tại O. Ta sẽ chứng minh AO là tia phân giác của góc A.
Kẻ các đường vuông góc OH, OI, OK từ O lần lượt đến các đường thẳng AB, BC, AC.
Vì BO là tia phân giác của góc HBC nên OH = OI (1)
Vì CO là tia phân giác của góc KCB nên OI = OK (2)
Từ (1) và (2) suy ra OI = OH = OK
(3)
Suy ra: O thuộc đường phân giác của góc BAC.
Suy ra AO là tia phân giác của góc BAC và ta có điều phải chứng minh.
CM
29 tháng 6 2017
- Các tính chất ở các câu a, b được suy ra từ định lí "Tổng ba góc của một tam giác bằng 180o".
* Chứng minh:
?4 bài 1 – trang 107.
20 tháng 4 2017
Các tính chất ở cá câu a ,b được suy ra từ định lí "Tổng ba góc của một tam giác bằng 180o".
Tính chất ở câu c được suy ra từ định lí "Trong một tam giác cân hai góc ở đáy bằng nhau".
Tính chất ở câu d được suy ra từ định lí: Nếu một tam giác có ba góc bằng nhau thì tam giác đo là tam giác cân.
20 tháng 4 2017
Các tính chất ở các câu (a); (b) được suy ra từ định lí: “Tổng ba góc của một tam giác bằng nhau bằng 1800”.
Tính chất ở câu (c) được suy ra từ định lí: “Trong tam giác cân, hai góc ở đáy bằng nhau”.
Tính chất ở câu (d) được suy ra từ định lí: “Nếu một tam giác có hai góc bằng nhau thì tam giác đó là tam giác cân”.
MT
2
MH
26 tháng 7 2015
vẽ tam giác ABC. gọi ABE là góc ngoài của \(\Delta ABC\)(vẽ góc ABE kề bù vs góc B)
ta có: ABE+B=1800(kề bù)
mà A+C+B=1800(tổng 3 góc trong tam giác)
=> ABE=A+C
=> góc ngoài của tam giác = tổng 2 góc trong ko kề với nó
TT
26 tháng 7 2015
Ta có
góc ngoài của tam giác = 180 độ - góc trong kề
2 góc trong không kề = 180 độ - góc trong kề với góc ngoài
nên góc ngoài của tam giác = 2 góc trong không kề
đơn giản vẽ hình đi
sach giao khoa lop 7 phan toan hinh ve tam giac y