Tam giác ABC có góc A + góc B = 90 độ. Tam giác ABC là tam giác gì ?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
25 tháng 2 2021
\(\widehat{AMC}=90^o\Rightarrow AM\perp BC\)
△ABC có AM là đường phân giác
AM là đường cao
⇒ △ABC cân tại A
21 tháng 12 2021
bài 2:
ta có: AB<AC<BC(Vì 3cm<4cm<5cm)
=> góc C>góc A> góc B (Các cạnh và góc đồi diện trong tam giác)
Bài 3:
*Xét tam giác ABC, có:
góc A+góc B+góc c= 180 độ( tổng 3 góc 1 tam giác)
hay góc A+60 độ +40 độ=180độ
=> góc A= 180 độ-60 độ-40 độ.
=> góc A=80 độ
Ta có: góc A>góc B>góc C(vì 80 độ>60 độ>40 độ)
=> BC>AC>AB( Các cạnh và góc đối diện trong tam giác)
LN
Lưu Nguyễn Hà An
CTVHS
15 tháng 2 2022
bài 2:
ta có: AB <AC <BC (Vì 3cm <4cm <5cm)
=> góc C>góc A> góc B (Các cạnh và góc đồi diện trong tam giác)
Bài 3:
*Xét tam giác ABC, có:
góc A+góc B+góc c= 180 độ( tổng 3 góc 1 tam giác)
hay góc A+60 độ +40 độ=180độ
=> góc A= 180 độ-60 độ-40 độ.
=> góc A=80 độ
Ta có: góc A>góc B>góc C(vì 80 độ>60 độ>40 độ)
=> BC>AC>AB( Các cạnh và góc đối diện trong tam giác)
HT mik làm giống bạn Dương Mạnh Quyết
19 tháng 1 2023
`a,` vì Tam giác `ABC` có \(\widehat{A}=110^0\)
`=>` Tam giác `ABC` là tam giác tù.
`b,` Cạnh đối diện của \(\widehat{A}\) là cạnh `BC`
`=>` Cạnh lớn nhất của Tam giác `ABC` là cạnh `BC`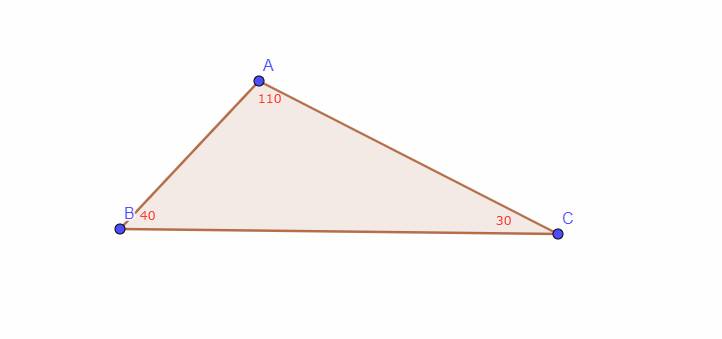
4 tháng 4 2021
Sửa đề: \(\widehat{A}=60^0\)
a) Xét ΔACE vuông tại C và ΔAKE vuông tại K có
AE chung
\(\widehat{CAE}=\widehat{KAE}\)(AE là tia phân giác của \(\widehat{CAK}\))
Do đó: ΔACE=ΔAKE(cạnh huyền-góc nhọn)
4 tháng 4 2021
b) Ta có: ΔABC vuông tại C(gt)
nên \(\widehat{CAB}+\widehat{CBA}=90^0\)(hai góc nhọn phụ nhau)
\(\Leftrightarrow\widehat{EBA}+60^0=90^0\)
\(\Leftrightarrow\widehat{EBA}=30^0\)(1)
Ta có: AE là tia phân giác của \(\widehat{CAB}\)(gt)
nên \(\widehat{EAB}=\dfrac{\widehat{CAB}}{2}=\dfrac{60^0}{2}=30^0\)(2)
Từ (1) và (2) suy ra \(\widehat{EBA}=\widehat{EAB}\)
Xét ΔEAB có \(\widehat{EBA}=\widehat{EAB}\)(cmt)
nên ΔEAB cân tại E(Định lí đảo của tam giác cân)
NH
13 tháng 6 2020
a, Xét △ABC vuông tại A có: ABC + ACB = 90o (tổng 2 góc nhọn trong △ vuông)
=> ABC + 30o = 90o => ABC = 60o
Vì BD là phân giác ABC => ABD = DBC = ABC : 2 = 60o : 2 = 30o
Xét △DBC có: DBC = DCB = 30o => △DBC cân tại D
b, Xét △ABD vuông tại A và △ACB vuông tại A
Có: ABD = ACB (= 30o)
=> △ABD ᔕ △ACB (g.g)
c, Xét △ABC vuông tại A có: BC2 = AB2 + AC2 (định lý Pytago)
=> BC2 = 62 + 82 => BC2 = 100 => BC = 10 (cm)
Vì BD là phân giác ABC
\(\Rightarrow\frac{AD}{AB}=\frac{DC}{BC}\) \(\Rightarrow\frac{AD}{6}=\frac{DC}{10}=\frac{AD+DC}{6+10}=\frac{AC}{16}=\frac{8}{16}=0,5\) (Áp dụng t/c dãy tỉ số bằng nhau)
Do đó: \(\frac{AD}{6}=0,5\)\(\Rightarrow AD=3\) (cm)
XÉT TAM GIÁC ABC
CÓ: \(\widehat{A}+\widehat{B}+\widehat{C}=180^0\) ( định lí)
THAY SỐ: \(90^0+\widehat{C}=180^0\)
\(\widehat{C}=180^0-90^0\)
\(\widehat{C}=90^0\)
\(\Rightarrow\Delta ABC\) VUÔNG TẠI C ( ĐỊNH LÍ)
CHÚC BN HỌC TỐT!!!!!!!!