Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


AB = AC => Tam giác ABC cân tại A
a. Xét tam giác AMB và tam giác AMC
AB = AC ( gt )
Góc B = góc C ( ABC cân )
BM = CM ( gt )
Vậy...... ( c.g.c)
=> góc BAM = góc CAM ( 2 góc tương ứng )
=> AM là phân giác góc A
b. trong tam giác cân ABC đường phân giác cũng là đường cao
=> AM vuông BC
c.tam giác MEF là tam giác cân vì:
xét tam giác vuông BME và tam giác vuông CMF
Góc B = góc C
MB = MC ( gt )
Vậy....( cạnh huyền. góc nhọn )
=> ME = MF ( 2 cạnh tương ứng )
Chúc bạn học tốt !!!
a: Xét ΔAMB và ΔAMC có
AM chung
MB=MC
AB=AC
Do đó: ΔAMB=ΔAMC
Ta có: ΔABC cân tại A
mà AM là đường trung tuyến
nên AM là đường phân giác
b: Ta có: ΔABC cân tại A
mà AM là đường trung tuyến
nên AM là đường cao
c: Xét ΔAEM vuông tại E và ΔAFM vuông tại F có
AM chung
\(\widehat{EAM}=\widehat{FAM}\)
Do đó: ΔAEM=ΔAFM
Suy ra: ME=MF
hay ΔMEF cân tại M

a: Xét ΔBAH vuông tại A và ΔBMH vuông tại M có
BH chung
góc ABH=góc MBH
=>ΔBAH=ΔBMH
b: BA=BM
HA=HM
=>BH là trung trực của AM
=>BH vuông góc AM
c: Xét ΔBMN vuông tại M và ΔBAC vuông tại A có
BM=BA
góc MBN chung
=>ΔMBN=ΔABC
=>BN=BC
Xét ΔBNC có BA/BN=BM/BC
nên AM//NC

a: ΔABM=ΔACM
=>BM=CM
=> M là trung điểm của BC
b: ΔAMC=ΔAMB
=>góc MAC=góc MAB và AC=AB
=>AM là phân giác của góc BAC
AB=AC
MB=MC
=>AM là trung trực của BC
=>AM vuông góc BC

a: Xét ΔAMC và ΔDMB có
MA=MD
góc AMC=góc DMB
MC=MB
=>ΔAMC=ΔDMB
b: ΔAMC=ΔDMB
=>góc MAC=góc MDB
=>AC//BD
=>BD vuông góc BA
=>ΔBAD vuông tại B
c: XétΔABC vuông tại A và ΔBAD vuông tại A có
AB chung
AC=BD
=>ΔABC=ΔBAD
d: AM=1/2BC
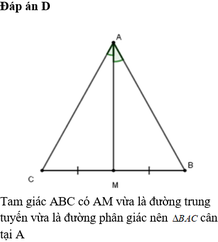
\(\widehat{AMC}=90^o\Rightarrow AM\perp BC\)
△ABC có AM là đường phân giác
AM là đường cao
⇒ △ABC cân tại A
thank you bạn alots