Tại sao có thể nói : Cộng hai số nguyên là trường hợp riêng của cộng hai phân số ? Cho ví dụ ?
Làm giúp mik với ? làm nhanh, đúng thì mình tik cho !
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
PT
1
CM
14 tháng 9 2017
Ta có thể nói: Cộng hai số nguyên là trường hợp riêng của cộng hai phân số vì mỗi số nguyên đều có thể viết đươc dưới dạng 1 phân số
Ví dụ:
10 tháng 3 2017
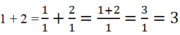
Vì cộng hai số nguyên còn viết dưới dang là a + b = \(\frac{a}{1}\)+\(\frac{b}{1}\) nên gọi là trường hợp riêng của cộng 2 phân số
VD: 2 + 3 =\(\frac{2}{1}\)+\(\frac{3}{1}\)
10 tháng 3 2017
Bởi vì số nguyên có thể viết dưới dạng phân số có tử là chính nó, mẫu là 1
tk nhé
TL
1
NT
1
22 tháng 2 2017
ta có mọi phân số có thể viết thành số nguyên gọi là số hữu tỷ
(=) tử của phân số đó chia hết cho mẫu
vì vậy cộng 2 số nguyên cũng chính là cộng 2 phân số có tử số chia hết cho mẫu số
VD: -10/2 + 100/-25 =-5 +-4=-9
bài này đúng 100% bạn nhé
BT
1
G
15 tháng 11 2017
1. Phép cộng Phép nhân
Tính chất giao hoán: a + b = b + a a x b = b x a
Tính chất kết hợp: ( a + b ) + c = a + ( b + c ) ( a x b ) x c = a x ( b x c )
Tính chất phân phối của phép
nhân đối với phép cộng : a x ( b + c ) = a x b + a x c
2. Lũy thừa bậc n của a là n số nhân với nhau, mỗi số có giá trị bằng a
3. am x an = am + n. Muốn nhân hai lũy thừa cùng cơ số, ta giữ nguyên cơ số rồi cộng các số mũ.
am : an = am - n ( m lớn hơn hoặc bằng n). Muốn chia hai lũy thừa cùng cơ số, ta giữ nguyên cơ số rồi trừ các số mũ.
4. Khi xuất hiện một số tự nhiên q mà a = b x q thì ta nói số tự nhiên a chia hết cho số tự nhiên b
5. Khi tất cả các số trong một tổng đều chia hết cho một số thì tổng đó chia hết cho số đó.
Nếu a chia hết cho m, b chia hết cho m thì a + b cũng chia hết cho m
k cho mình, 15 phút nữa mình giải tiếp, bạn đăng nhiều quá !
15 tháng 11 2017
Ban Gauss oi ngay mai minh k cho nhe bay gio muon roi minh phai ngu
Tại vì mọi số nguyên a + b đều được viết dưới dạng \(\frac{a}{1}+\frac{b}{1}\)
VD : 50 + 10 = \(\frac{50}{1}+\frac{10}{1}\)
Bởi vì số nguyên có thể viết dưới dạng phân số có tử là chính nó, mẫu là 1
tk nhé