Làm g mình từ câu c ạ
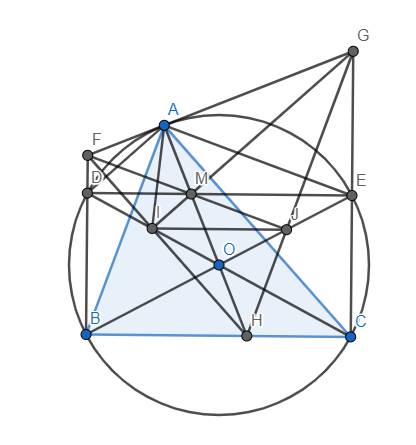
cho dường tròn (o) dây bc cố định không qua tâm, a là 1 điểm trên cung lớn ab sao cho tam giác abc nhọn, đường cao bi, ck cắt nhau tại h. và lần lượt cắt đường tròn tại e và f.
a) chứng minh bkic nội tiếp
b)ik//ef
c) oa vuông góc ik
d) Khi a di chuyển trên cung lớn cchứng minh ah ó độ dài không đổi