Giúp em bài hình này với ạ 
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
Vẽ hình và làm giúp em bài này với ạ, Em cảm ơn ạ
11 tháng 4 2023
a: góc CAO+góc CMO=180 độ
=>CAOM nội tiếp
b: Xét (O) có
CA,CM là tiếp tuyến
=>CA=CM và OC là phân giác của góc MOA(1)
Xét (O) co
DM,DB là tiếp tuyến
=>DM=DB và OD là phân giác của góc MOB(2)
CD=CM+MD=CA+DB
Từ (1), (2) suy ra góc COD=1/2*180=90 độ
c: AC*BD=CM*MD=OM^2=R^2
NH
2
16 tháng 11 2023
( Hình em tự vẽ nhé )
+ Ta có: ΔABC = ΔDEF
=> \(\widehat{A}=\widehat{D}=30^o\)
+ Ta có: \(2\widehat{B}=3\widehat{C}\)
=> \(\widehat{B}=\dfrac{3\widehat{C}}{2}\)
+ Xét ΔABC
=> \(\widehat{A}+\widehat{B}+\widehat{C}=180^o\left(t3g\Delta\right)\)
Mà \(\widehat{A}=30^o;\widehat{B}=\dfrac{3\widehat{C}}{2}\)
=> \(30^o+\dfrac{3\widehat{C}}{2}+\widehat{C}=180^o\)
=> \(\dfrac{3\widehat{C}}{2}+\widehat{C}=150^o\)
\(\Rightarrow\dfrac{3\widehat{C}}{2}+\dfrac{2\widehat{C}}{2}=150^o\)
\(\Rightarrow\dfrac{5\widehat{C}}{2}=150^o\)
\(\Rightarrow5\widehat{C}=75^o\)
\(\Rightarrow\widehat{C}=15^o\)
+ Xét ΔABC
\(\Rightarrow\widehat{A}+\widehat{B}+\widehat{C}=180^o\left(t3g\Delta\right)\)
\(\Rightarrow30^o+15^o+\widehat{B}=180^o\)
\(\Rightarrow\widehat{B}=135^o\)
16 tháng 11 2023
Do chị ko có máy ở đây nên ko chụp hình vẽ đc, em thông cảm nhé😢
KS
4 tháng 8 2023
có : \(AH\perp BD\)
\(CK\perp DB\) =>AH//CK
Có : tứ giác ABCD là hình bình hành :
`=>` AB//CB
`=> góc ADB = góc gocd DBC
Xét tam giác `ADH` và tam giác `CBK` có
`AB = CB`(tứ giác ABCD là hbh)
`AHD = CKB = 90^0`
`ADH = CBK(c/mt)`
`=> tam giác ADH = tam giác BCK(ch-gn)
`=> AH = CK`(t/ứng)
xét tg BHCK có :
`AH = Ck`
`AH//CK`
`=> tg BHCK là hình bình hành
1 tháng 2
a: Xét tứ giác APMQ có \(\widehat{APM}+\widehat{AQM}=90^0+90^0=180^0\)
nên APMQ là tứ giác nội tiếp đường tròn đường kính AM
Tâm O là trung điểm của AM
b: Ta có: ΔAHM vuông tại H
=>H nằm trên đường tròn đường kính AM
=>H nằm trên (O)
Ta có: ΔABC đều
mà AH là đường cao
nên AH là phân giác của góc BAC
Xét (O) có
\(\widehat{PAH}\) là góc nội tiếp chắn cung PH
\(\widehat{QAH}\) là góc nội tiếp chắn cung QH
\(\widehat{PAH}=\widehat{QAH}\left(cmt\right)\)
Do đó: \(sđ\stackrel\frown{HP}=sđ\stackrel\frown{HQ}\)
Xét (O) có
\(\widehat{QPH}\) là góc nội tiếp chắn cung QH
\(\widehat{HQP}\) là góc nội tiếp chắn cung HP
\(sđ\stackrel\frown{QH}=sđ\stackrel\frown{HP}\)
Do đó: \(\widehat{HPQ}=\widehat{HQP}\)
=>HQ=HP
=>H nằm trên đường trung trực của QP(1)
Ta có: OP=OQ
=>O nằm trên đường trung trực của QP(2)
Từ (1) và (2) suy ra HO là đường trung trực của PQ
=>HO\(\perp\)PQ
7 tháng 4 2023
a: Xet ΔBAE vuông tại A và ΔBDE vuông tại D có
BE chung
BA=BD
=>ΔBAE=ΔBDE
=>AE=DE
mà BA=BD
nên BE là trung trực của AD
b: góc HAD+góc BDA=90 độ
góc CAD+góc BAD=90 độ
góc BAD=góc BDA
=>góc HAD=góc CAD
=>AD là phân giác của góc HAC
c: Xét ΔAHC có AD là phân giác
nên AH/AC=HD/DC
mà AH<AC
nên HD<DC
HK
1
27 tháng 7 2023
a: góc AEB=góc ADB=90 độ
=>AEDB nội tiếp đường tròn đường kính AB
=>I là trung điểm của AB
b: Gọi H là giao của AD và BE
ABDE nội tiếp
=>góc HDE=góc HBA
=>góc HDE=góc HMN
=>DE//MN
KM
0
HN
2
26 tháng 8 2021
a: Xét ΔABD và ΔHBD có
BA=BH
\(\widehat{ABD}=\widehat{HBD}\)
BD chung
Do đó: ΔABD=ΔHBD
b: Ta có: ΔABD=ΔHBD
nên \(\widehat{BAD}=\widehat{BHD}\)
mà \(\widehat{BAD}=90^0\)
nên \(\widehat{BHD}=90^0\)
hay DH\(\perp\)BC
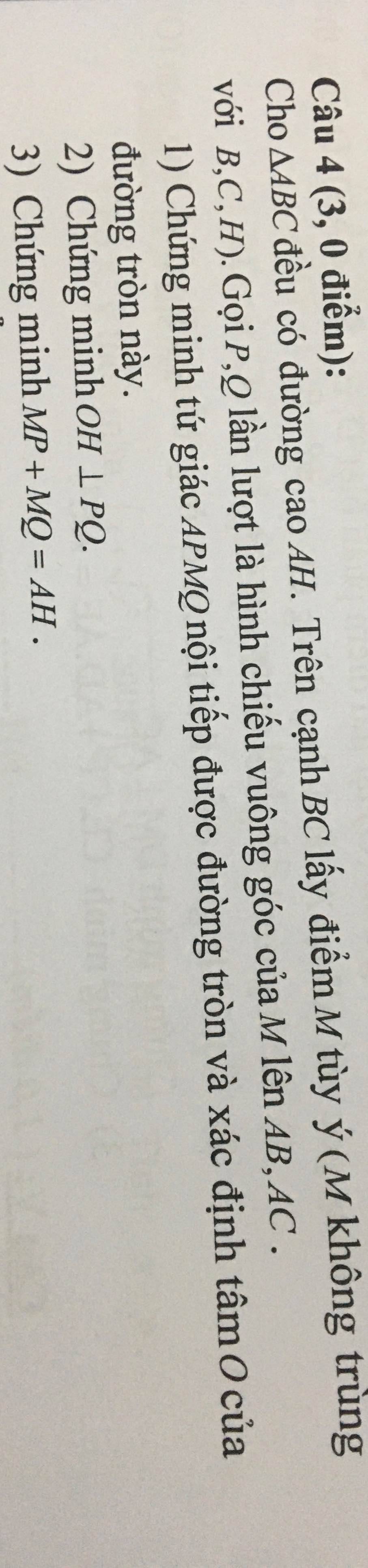
a)Ta có:
`hat{BFC}` là góc chẵn nửa (O)
`=>hat{BFC}=90^o`
Tương tự:`hat{BEC}=90^o`
Xét tam giác ABC có:
`CFbotAB(CMT)`
`AEbotAC(CMT)`
Mà CF cắt BE tại H
`=>H` là trực tâm tam giác ABC
`=>AHbotBC`
Hay `AD bot BC`
Vì `hat{BFH}=hat{BDH}=90^o`
`=>hat{BFH}+hat{BDH}=180^o`
`=>` tg BFHD nt
`=>hat{DFC}=hat{DBE}`
b)Vì `hat{EBC}=hat{EFC}`(cùng chắn cung EC nhỏ)
Mà tg BFHD nt
`=>hat{DFH}=\hat{HBD}`
`=>hat{DFH}=hat{EFC}`
`=>` FC là pg `hat{EFD}`
Vì `FC` là pg `hat{EFD}`
`=>hat{EFD}=2hat{DFH}`
Mà `hat{DFH}=hat{HBD}`
`=>hat{EFD}=2hat{DBH}`
Mà `hat{EOC}=2hat{DBH}`(góc nội tiếp và góc ở tâm)
`=>hat{EFD}=hat{EOC}`
`=>` tg OEFD nt (do trong = góc ngoài tại đỉnh đối)