Cho tam giác ABC cân tại A,góc A = 120 độ.Vẽ tia Cx sao choCB là tia phân giác của góc ACx.Vẽ AH vuông góc Cx
a)tính góc HAC
b)CMR:AH =1/2 BC
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
DT
9 tháng 3 2022
Có gì khong hiểu hỏi lại cj nhé:
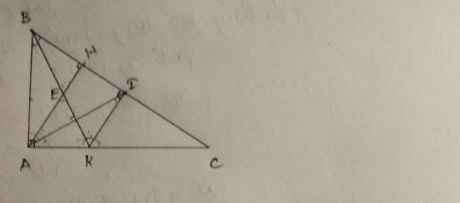
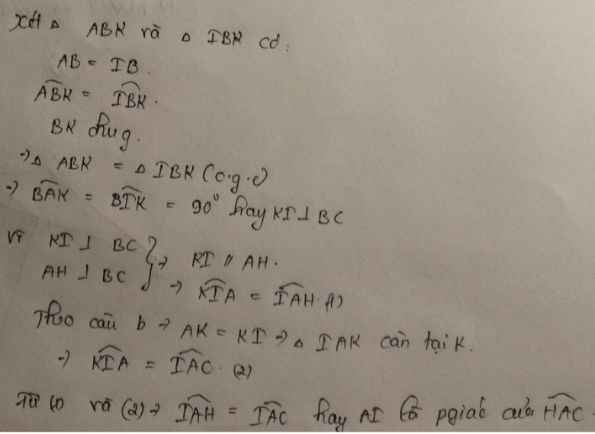
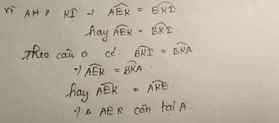
a, b ,c lần lượt từ trên xuống.
27 tháng 6 2023
a: Xét ΔAHD và ΔAID có
AH=AI
góc HAD=góc IAD
AD chung
=>ΔAHD=ΔAID
=>góc HAD=góc IAD
=>AD là phân giác của góc HAC
b: ΔAHD=ΔAID
=>góc AID=góc AHD=90 độ
Xét ΔDHM vuông tại H và ΔDIC vuông tại I có
DH=DI
góc HDM=góc IDC
=>ΔDHM=ΔDIC
=>MD=MC
c: AH+HM=AM
AI+IC=AC
mà AH=AI và HM=IC
nên AM=AC
=>ΔAMC cân tại A
mà AN là trung tuyến
nên AN vuông góc MC
Xét ΔCAM có
AN,MI,CH là đường cao
=>AN,MI,CH đồng quy
=>AN,MI,BC đồng quy
5 tháng 4 2022
Bài 2:
a: Xét ΔAHB và ΔAHC có
AB=AC
\(\widehat{BAH}=\widehat{CAH}\)
AH chung
DO đó; ΔAHB=ΔAHC
b: Ta có: ΔABC cân tại A
mà AH là đường phân giác
nên AH là đường cao
c: BC=10cm nên BH=CH=5cm
=>AC=13cm
À hình đây :
a, Ta có : \(\widehat{A}+\widehat{B}+\widehat{C}=180^o\)
Mà \(\Delta ABC\)cân tại A .
=> \(\widehat{A}+2\widehat{C}=180^o\)
Hay \(120^o+2\widehat{C}=180^o\)
=> \(\widehat{C}=30^o\)
Mà \(CB\)là tia phân giác của \(\widehat{ACx}\)
=> \(\widehat{ACx}=\widehat{C_1}+\widehat{C_2}=30^o+30^o=60^o\)
Áp dụng định lí tổng ba góc trong tam giác vuông AHC , ta có :
\(\widehat{ACx}+\widehat{HAC}=90^o\)
\(\Leftrightarrow60^o+\widehat{HAC}=90^o\)
\(\Leftrightarrow\widehat{HAC}=30^o\)
b,
Kẻ \(AK\perp BC\)
Xét \(\Delta\perp AKC\)và \(\Delta\perp CHA\)có :
\(\widehat{HAC}=\widehat{C_1}\left(=30^o\right)\)
Cạnh chung AC
=> \(\Delta\perp AKC\)=\(\Delta\perp CHA\)( cạnh huyền và góc nọn kề cạnh ấy )
=> AH=KC ( hai cạnh tương ứng )
Ta có : \(\Delta ABC\)( cân tại A ) có AH là đường cao
=> AH cũng là đường trung tuyến của \(\Delta ABC\)
=> BK=KC
=> KC=1/2BC
mà KC=AH
=> AH=1/2BC