Question

[nguyen duc hung]

Bài 28 (trang 22 SGK Toán 9 tập 2): Tìm hai số tự nhiên, biết rằng tổng của chúng bằng 1006 và nếu lấy số lớn chia cho số nhỏ thì được thương là 2 và số dư là 124.

Bài 29 (trang 22 SGK Toán 9 tập 2): Giải bài toán cổ sau:

Quýt, cam mười bảy quả tươi

Đem chia cho một trăm người cùng vui

Chia ba mỗi quả quýt rồi

Còn cam mỗi quả chia mười vừa xinh

Trăm người, trăm miếng ngọt lành

Quýt, cam mỗi loại tính rành là bao?

Answer 1

[Nguyễn Gia Phong]

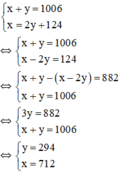
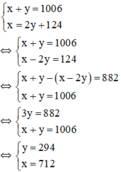
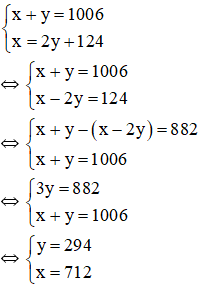
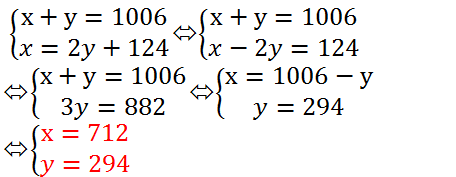
Bài 28

Đặt sô cần tìm là a và b (a>b)

ta có a+b=1006=> a=1006-b 

a=b*2+124=> 1006-b= b*2 +124 => b= 294=> a= 712

bài 29

Gọi số cam là a

số quýt là b

ta có a+b=17=> a=17-b

3*b+a*10=100 

=> 3*b+10*(17-b) = 100 => b=10=> a=7

Answer 2

[KAl(SO4)2·12H2O]

Bài 28:

Gọi số lớn là x, số nhỏ là y (a, y ∈ N*); x > 124. Ta có: Tổng bằng 1006 nên được: x + y = 1006

Số lớn chia số nhỏ được thương là 2, số dư là 124 nên ta có điều kiện là y > 124 và có phương trình: x = 2y + 124

Ta có HPT:

\(\hept{\begin{cases}x+y=1006\\x=2y+124\end{cases}\Leftrightarrow\hept{\begin{cases}x+y=1006\\x-2y=124\end{cases}}}\)

Vậy hai số tự nhiên phải tìm là 712 và 294.

Bài 29:

Gọi số cam là x, số quýt là y. Điều kiện x, y là số nguyên dương.

Theo đề bài, ta có HPT: \(\hept{\begin{cases}x+y=17\left(1\right)\\10x+3y=100\left(2\right)\end{cases}}\)

\(\text{PT}\left(1\right)\Leftrightarrow y=17-x\)

Thế (3) vào (2): 10x + 3(17 - x) = 100

<=> 10x + 51 - 3x = 100 <=> 7x = 49 <=> x = 7

=> y = 17 - 7 = 10

=> Có 7 quả cam và 10 quả quýt.