Giải và biện luận pt
m*2x - m*2 = 4x - 3m + 2
Dấu * là dấu mũ đó nha
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.




m2x + 6 = 4x + 3m
⇔ m2.x – 4x = 3m – 6
⇔ (m2 – 4).x = 3m – 6 (2)
+ Xét m2 – 4 ≠ 0 ⇔ m ≠ ±2, phương trình (2) có nghiệm duy nhất:
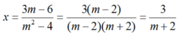
+ Xét m2 – 4 = 0 ⇔ m = ±2
● Với m = 2, pt (2) ⇔ 0x = 0 , phương trình có vô số nghiệm
● Với m = –2, pt (2) ⇔ 0x = –12, phương trình vô nghiệm.
Kết luận:
+ m = 2, phương trình có vô số nghiệm
+ m = –2, phương trình vô nghiệm
+ m ≠ ±2, phương trình có nghiệm duy nhất 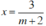


Kết luận:
Với m > 0 phương trình có nghiệm là x = 2m.
Với m = 0 phương trình có nghiệm là mọi số thực không âm.
Với m < 0 phương trình vô nghiệm.

a) ⇔ (m – 3)x = 2m + 1.
b) ⇔ (m2 – 4)x = 3m – 6.
c) ⇔ 2(m – 1)x = 2(m-1).
Phương trình ẩn x : \(m^2x-m^2=4x-3m+2\)( 1 )
\(m^2x-4x=m^2-3m+2\)
\(\left(m^2-4\right)x=\left(m-1\right)\left(m-2\right)\)
- Nếu \(m^2-4\ne0\Leftrightarrow m^2\ne4\Leftrightarrow m\ne\pm2\)
Thì phương trình ( 1 ) có nghiệm duy nhất:
\(x=\frac{\left(m-1\right)\left(m-2\right)}{\left(m-2\right)\left(m+2\right)}=\frac{m-1}{m+2}\)
- Nếu \(m^2-4=0\Leftrightarrow m^2=4\Leftrightarrow m=\pm2\)
- Xét m = 2 thì phương trình ( 1 ) có dạng:
\(\left(2^2-4\right)x=\left(2-1\right)\left(2-2\right)\Leftrightarrow0x=0\)phương trình vô số nghiệm
- Xét m = -2 thì phương trình ( 1 ) có dạng
\(\left[\left(-2\right)^2-4\right]x=\left(-2-1\right)\left(-2-2\right)\)
\(\Leftrightarrow0x=12\)phương trình vô nghiệm
Vậy: Nếu \(m\ne\pm2\) thì phương trình ( 1 ) có nghiệm duy nhất \(x=\frac{m-1}{m+2}\)
Nếu m = 2 thì phương trình ( 1 ) vô số nghiệm
Nếu m = -2 thì phương trình ( 1 ) vô nghiệm