Cho tam giác ABC có đường cao AH,đường phân giác AD;góc A=\(80^o\),góc C=\(60^o\).Tính HAD
(NẾU AI NHANH NHẤT MÌNH SẼ tick CHO)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
11 tháng 7 2023
ΔAHE vuông tại H nên AH<AE
=>góc AEH<90 độ
=>góc AED>90 độ
=>AE<AD
=>AH<AE<AD
13 tháng 6 2021
a, Áp dụng định lí Pytago cho tam giác ABC vuông tại A
\(AB^2+AC^2=BC^2\Rightarrow BC^2=\left(\frac{3}{5}BC\right)^2+AC^2\)
\(\Leftrightarrow AC^2=\frac{16}{25}BC^2\Leftrightarrow AC=\frac{4}{5}BC\)
* Áp dụng hệ thức :
\(\frac{1}{AH^2}=\frac{1}{AB^2}+\frac{1}{AC^2}\Rightarrow\frac{1}{144}=\frac{1}{\frac{9}{25}BC^2}+\frac{1}{\frac{16}{25}BC^2}\)
\(\Leftrightarrow\frac{1}{144}=\frac{\frac{16}{25}BC^2+\frac{9}{25}BC^2}{\frac{16}{25}BC^2.\frac{9}{25}BC^2}\Rightarrow144BC^2=\frac{144}{625}BC^4\)
\(\Leftrightarrow\frac{144}{625}BC^2-144=0\Leftrightarrow BC^2=144.\frac{625}{144}=625\Leftrightarrow BC=25\)cm
\(\Rightarrow AB=\frac{3}{5}BC=\frac{3}{5}.25=\frac{75}{5}=15\)cm
\(\Rightarrow AC=\frac{4}{5}BC=\frac{4}{5}.25=\frac{100}{5}=20\)
Chu vi tam giác là : \(P_{ABC}=AB+BC+AB=15+20+25=60\)cm2
13 tháng 6 2021
b, Vì AD là phân giác nên : \(\frac{AB}{AC}=\frac{BD}{DC}=\frac{15}{20}=\frac{3}{4}\Rightarrow AB=\frac{3}{4}AC\)
Lại có : \(BC=BD+DC=15+20=35\)cm
Áp dụng định lí Pytago cho tam giác ABC vuông tại A
\(BC^2=AC^2+AB^2=AC^2+\left(\frac{3}{4}AC\right)^2\)
\(\Rightarrow\frac{25}{16}AC^2=1225\Leftrightarrow AC^2=\frac{16.1225}{25}=784\Leftrightarrow AC=28\)cm
\(\Rightarrow AB=\frac{3}{4}.28=21\)cm
* Áp dụng hệ thức : \(\frac{1}{AH^2}=\frac{1}{AB^2}+\frac{1}{AC^2}\Rightarrow\frac{1}{AH^2}=\frac{AC^2+AB^2}{AB^2AC^2}\)
\(\Leftrightarrow\frac{1}{AH^2}=\frac{784+441}{345744}\Leftrightarrow1225AH^2=345744\Leftrightarrow AH^2=\frac{7056}{25}\Leftrightarrow AH=\frac{84}{5}\)cm
* Áp dụng hệ thức : \(AB^2=BH.BC\Rightarrow BH=\frac{AB^2}{BC}=\frac{441}{35}=\frac{63}{5}\)cm
\(\Rightarrow HD=BD-BH=15-\frac{63}{5}=\frac{12}{5}\)cm
Áp dụng định lí Pytago cho tam giác AHD vuông tại H
\(AD^2=AH^2+HD^2=\left(\frac{84}{5}\right)^2+\left(\frac{12}{5}\right)^2=288\Rightarrow AD=12\sqrt{2}\)cm
12 tháng 7 2023
1:
BC=15+20=35cm
AD là phân gíac
=>AB/BD=AC/CD
=>AB/3=AC/4=k
=>AB=3k; AC=4k
AB^2+AC^2=BC^2
=>25k^2=35^2
=>k=7
=>AB=21cm; AC=28cm
AH=21*28/35=16,8cm
\(AD=\dfrac{2\cdot21\cdot28}{21+28}\cdot cos45=12\sqrt{2}\left(cm\right)\)
2:
BC=căn 12^2+16^2=20cm
HB=AB^2/BC=12^2/20=7,2cm
HC=20-7,2=12,8cm
29 tháng 3 2023
a: Xét ΔAHB vuông tại H và ΔCHA vuông tạiH có
góc HAB=góc HCA
=>ΔAHB đồng dạng với ΔCHA
c: BK là phân giác
=>AK/CK=BA/BC
ΔAHC có AD là phân giác
nên DH/CD=AH/AC=BA/BC
=>DH/CD=AK/CK
=>KD//AH
CM
2 tháng 12 2019
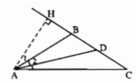
+) Ta có: ∠(ABH) + ∠(ABC) = 180º ( hai góc kề bù)
Suy ra: ∠(ABH) = 180º - ∠(ABC) = 180º − 112º = 68º
+) Xét tam giác AHB vuông tại H ta có:
∠A1+ ∠(ABH) = 90º ( tính chất tam giác vuông)
Suy ra: ∠A1= 90º − ∠(ABH) = 90º − 68º = 22º
+) Tam giác ABC cân tại B nên ∠(BAC) = ∠(ACB)
Lại có ∠(ABC) = 112º và ∠(BAC)+ ∠(ACB) + ∠(ABC) = 180º nên
∠(BAC) = (180º − 112º) : 2 = 34o
+) Do AD là tia phân giác của góc BAC nên
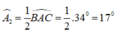
+ Từ đó
∠(HAD) = ∠A1 + ∠A2= 22º + 17º = 39º.
Tam giác HAD vuông tại H nên: ∠(HDA)+ ∠(HAD) = 90º
Suy ra: ∠(HDA) = 90º − ∠(HAD) = 90º − 39º = 51º
CHA và đường phân giác BK của tam giác ABC (D thuộc BC; K thuộc AC). BK cắt lần lượt AH và AD tại E và F.
MT
22 tháng 7 2018
BÀI 1:
a)
· Trong ∆ ABC, có: AB2= BC.BH
Hay BC= 
= 
· Xét ∆ ABC vuông tại A, có:
AB2= BH2+AH2
↔AH2= AB2 – BH2
↔AH= 
=4 (cm)
b)
· Ta có: HC=BC-BH
àHC= 8.3 - 3= 5.3 (cm)
· Trong ∆ AHC, có:
· 
KT
22 tháng 7 2018
Bài 1:
a) Áp dụng hệ thức lượng ta có:
\(AB^2=BH.BC\)
\(\Rightarrow\)\(BC=\frac{AB^2}{BH}\)
\(\Rightarrow\)\(BC=\frac{5^2}{3}=\frac{25}{3}\)
Áp dụng Pytago ta có:
\(AH^2+BH^2=AB^2\)
\(\Rightarrow\)\(AH^2=AB^2-BH^2\)
\(\Rightarrow\)\(AH^2=5^2-3^2=16\)
\(\Rightarrow\)\(AH=4\)
b) \(HC=BC-BH=\frac{25}{3}-3=\frac{16}{3}\)
Áp dụng hệ thức lượng ta có:
\(\frac{1}{HE^2}=\frac{1}{AH^2}+\frac{1}{HC^2}\)
\(\Leftrightarrow\)\(\frac{1}{HE^2}=\frac{1}{4^2}+\frac{1}{\left(\frac{16}{3}\right)^2}=\frac{25}{256}\)
\(\Rightarrow\)\(\frac{1}{HE}=\frac{5}{16}\)
\(\Rightarrow\)\(HE=\frac{16}{5}\)
( Hình chỉ mang tính chất hư cấu :v )
Vì AH là phân giác \(\widehat{CAB}\)nên \(\widehat{BAD}=\frac{\widehat{CAB}}{2}=\frac{80^o}{2}=40^o\)
Xét \(\Delta ABC:\)
\(\widehat{CAB}+\widehat{ABC}+\widehat{ACB}=180^o\)( Tổng ba góc trong tam giác )
\(\Rightarrow\widehat{ABC}+80^o+60^o=180^o\)
\(\Rightarrow\widehat{ABC}=40^o\)
\(\Rightarrow\widehat{ABD}=40^o\)( Do \(D\in BC\))
Xét \(\Delta ABD:\)
\(\widehat{ABD}+\widehat{ADB}+\widehat{BAD}=180^o\)(Tổng ba góc trong tam giác )
\(\Rightarrow\widehat{ADB}+40^o+40^o=180^o\)
\(\Rightarrow\widehat{ADB}=100^o\)
Xét \(\Delta HAD\)có \(\widehat{ADB}\)là góc ngoài đỉnh \(D\)
\(\Rightarrow\widehat{HAD}+\widehat{AHD}=\widehat{ADB}=100^o\)
\(\Rightarrow\widehat{HAD}+90^o=100^o\)
\(\Rightarrow\widehat{HAD}=10^o\)
Vậy ...