Cho hàm số bậc hai \(y = f(x) = {x^2} - 4x + 3\)
a) Xác định hệ số a. Tính \(f(0);f(1);f(2);f(3);f(4)\) và nhận xét về dấu của chúng so với dấu của hệ số a
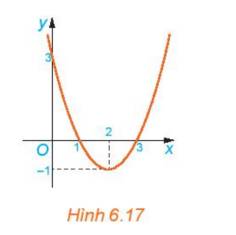
b) Cho đồ thị hàm số y=f(x) (H.6.17). Xét từng khoảng \(\left( { - \infty ;1} \right);\left( {1;3} \right);\left( {3; + \infty } \right)\), đồ thị nằm phía trên hay phía dưới trục Ox?
c) Nhận xét về dấu của f(x) và dấu của hệ số a trên từng khoảng đó.


a) Hệ số a là: a=1
\(f(0) = {0^2} - 4.0 + 3 = 3\)
\(f(1) = {1^2} - 4.1 + 3 = 0\)
\(f(2) = {2^2} - 4.2 + 3 = - 1\)
\(f(3) = {3^2} - 4.3 + 3 = 0\)
\(f(4) = {4^2} - 4.4 + 3 = 3\)
=> f(0); f(4) cùng dấu với hệ số a; f(2) khác dấu với hệ số a
b) Nhìn vào đồ thị ta thấy
- Trên khoảng \(\left( { - \infty ;1} \right)\) đồ thị nằm phía trên trục hoành
- Trên khoảng \(\left( {1;3} \right)\), đồ thị nằm phía dưới trục hoành
- Trên khoảng \(\left( {3; + \infty } \right)\), đồ thị nằm phía trên trục hoành
c) - Trên khoảng \(\left( { - \infty ;1} \right)\) đồ thị nằm phía trên trục hoành => f(x)>0, cùng dầu với hệ số a
- Trên khoảng \(\left( {1;3} \right)\), đồ thị nằm phía dưới trục hoành => f(x) <0, khác dấu với hệ số a
- Trên khoảng \(\left( {3; + \infty } \right)\), đồ thị nằm phía trên trục hoành => f(x)>0, cùng dấu với hệ số a