viến giả thiến , kến luận và hình cho tam giác abc có ab = ac. gọi I là trung điểm của bc.
a) chứng minh : tam giác aib= tam giác aic
b) chứng minh : ai là tia phân giác của góc bac
c) cho a =40°; b=70°. tính số đo của góc c
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét ΔAIB và ΔAIC có
AI chung
IB=IC
AB=AC
Do đó: ΔAIB=ΔAIC

a: Xét ΔAIB và ΔAIC có
AI chung
IB=IC
AB=AC
Do đó: ΔAIB=ΔAIC

\(\text{#TNam}\)
`a,` Vì Tam giác `ABC` cân tại `A -> AB = AC,`\(\widehat{B}=\widehat{C}\)
Xét Tam giác `AIB` và Tam giác `AIC` có:
`AB = AC (CMT)`
\(\widehat{B}=\widehat{C}\) `(CMT)`
`IB = IC (g``t)`
`=> \text {Tam giác AIB = Tam giác AIC (c-g-c)}`
Hnhu câu `b,` bạn ghi thiếu yêu cầu rồi nhé!
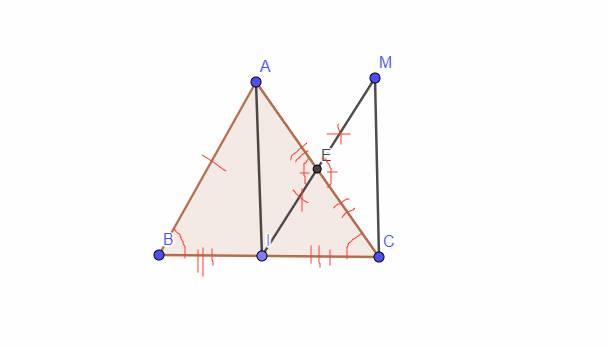
`c,` Xét Tam giác `AEI` và Tam giác `MEC` có:
`EA = EC (g``t)`
\(\widehat{AEI}=\widehat{MEC}\) `(\text {2 góc đối đỉnh})`
`EM = EI (g``t)`
`=> \text {Tam giác AEI = Tam giác MEC (c-g-c)}`
`->`\(\widehat{AIE}=\widehat{CME}\) `(\text {2 góc tương ứng})`
Mà `2` góc này nằm ở vị trí sole trong `-> \text {AI // CM}`
Vì Tam giác `ABI =` Tam giác `ACI (a)`
`->`\(\widehat{AIB}=\widehat{AIC}\) `(\text {2 góc tương ứng})`
Mà `2` góc này nằm ở vị trí kề bù
`->`\(\widehat{AIB}+\widehat{AIC}=180^0\)
`->`\(\widehat{AIB}=\widehat{AIC}=\) `180/2=90^0`
`-> AI \bot BC`
Mà `\text {AI // CM} -> MC \bot BC`

a: Xét ΔAIB và ΔAIC có
AB=AC
\(\widehat{BAI}=\widehat{CAI}\)
AI chung
Do đó: ΔAIB=ΔAIC
b: ΔAIB=ΔAIC
=>IB=IC và \(\widehat{AIB}=\widehat{AIC}\)
mà \(\widehat{AIB}+\widehat{AIC}=180^0\)(hai góc kề bù)
nên \(\widehat{AIB}=\widehat{AIC}=\dfrac{180^0}{2}=90^0\)
=>AI\(\perp\)BC
b: Xét ΔAHI vuông tại H và ΔAKI vuông tại K có
AI chung
\(\widehat{HAI}=\widehat{KAI}\)
Do đó: ΔAHI=ΔAKI
=>IH=IK
c: Xét ΔHIN vuông tại H và ΔKIM vuông tại K có
IH=IK
\(\widehat{HIN}=\widehat{KIM}\)
Do đó: ΔHIN=ΔKIM
=>IN=IM và HN=KM
ΔAHI=ΔAKI
=>AH=AK
AH+HN=AN
AK+KM=AM
mà AH=AK và HN=KM
nên AN=AM
=>A nằm trên đường trung trực của NM(1)
IN=IM(cmt)
nên I nằm trên đường trung trực của MN(2)
PN=PM
=>P nằm trên đường trung trực của MN(3)
Từ (1),(2),(3) suy ra A,I,P thẳng hàng

a: Xét ΔAIB và ΔAIC có
AI chung
IB=IC
AB=AC
Do đó: ΔAIB=ΔAIC
b: Ta có: ΔABC cân tại A
mà AI là đường trung tuyến
nên AI là đường cao
Ta có: I là trung điểm của BC
nên IB=IC=3cm
=>AI=4cm

a: Xét ΔABC có AB=AC
nên ΔABC cân tại A
hay \(\widehat{ABH}=\widehat{ACH}\)

5:
a: Xét ΔANB và ΔAMC có
AN=AM
góc BAN chung
AB=AC
=>ΔANB=ΔAMC
b: Xét ΔABC có AN/AC=AM/AB
nên MN//BC
c: góc ABN+góc IBC=góc ABC
góc ACM+góc ICB=góc ACB
mà góc ABN=góc ACM và góc ABC=góc ACB
nên góc IBC=góc ICB
=>IB=IC
mà AB=AC
nên AI là trung trực của BC
=>A,I,D thẳng hàng
a: Xét ΔAIB và ΔAIC có
AI chung
AB=AC
IB=IC
Do đó: ΔAIB=ΔAIC