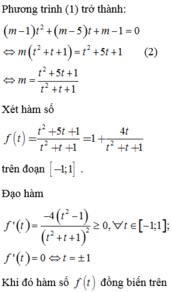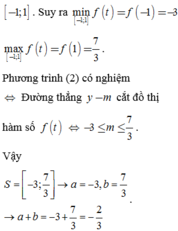cho a=4m;b=5mTính Gía trị biểu thức \(\frac{^{a^2+2b^2-m^2}}{a^2+3b^2-6m^2}\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
M
0
20 tháng 6 2019
Ta có: a, b là các số tự nhiên không chia hết cho 5
=> Chữ số cuối cùng các số a, b có thể là 1, 2, 3, 4, 6, 7, 8,9
mà 1^4=1, 2^4=16, 3^4 =81, 4^4=256, 6^41296,...
=> Như vậy chữ số tận cùng các sô a^4 và b^4 là 1 hoặc 6
=> Chữ số tận cùng các số a^4m, b^4m là 1 hoặc 6
=> Chữ số tận cùng các số a^4m -1 và b^4m -1 là 0 hoặc 5
=> \(\hept{\begin{cases}a^{4m}-1⋮5\\b^{4m}-1⋮5\end{cases}\Rightarrow}\hept{\begin{cases}x\left(a^{4m}-1\right)⋮5\\y\left(b^{4m}-1\right)⋮5\end{cases}}\)
=> \(x\left(a^{4m}-1\right)+y\left(b^{4m}-1\right)⋮5\Rightarrow xa^{4m}+yb^{4m}+\left(x+y\right)⋮5\Rightarrow xa^{4m}+yb^{4m}⋮5\)vì x+y chia hết cho 5
20 tháng 6 2019
Hoặc nếu em đã được học kiến thức đồng dư:
a, b là các số không chia hết cho 5
=> a^4 , b^4 có chữ số tận cùng là 1, 6
=> a^4m, b^4m có chữ số tận cùng 1, 6
=> \(\hept{\begin{cases}a^{4m}\equiv1\left(mod5\right)\\b^{4m}\equiv1\left(mod5\right)\end{cases}\Leftrightarrow}\hept{\begin{cases}x.a^{4m}\equiv x\left(mod5\right)\\y.b^{4m}\equiv y\left(mod5\right)\end{cases}\Rightarrow x.a^{4m}+y.b^{4m}\equiv x+y\equiv}0\left(mod5\right)\)
24 tháng 8 2016
a. [ H+] trong A: 2.2.10-4 + 6.10-4 = 10-3 mol pH = 3
[OH-] trong B: 3.10-4 + 2.3,5.10-4 = 10-3 mol pOH = 3 ® pH =11
b. Trong 300ml dung dịch A có số mol H+ = 0,3.10-3 mol Trong 200 ml dung dịch B có số mol OH- = 0,2.10-3 mol
Dung dịch C có: V = 0,5 lít; số mol H+ = 0,3.10-3 - 0,2.10-3 = 10-4 mol
Dạng 2: Pha trộn dung dịch
Phương pháp giải
+ Sử dụng phương pháp đường chéo, ghi nhớ: Nước có C% hoặc CM =0.
+ Xác định số mol chất, pH ® [H+]® mol H+ hoặc mol OH-.
+ Việc thêm, cô cạn nước làm thay đổi nồng độ mol/l và không làm thay đổi số mol chất
® tính toán theo số mol chất.
AH
Akai Haruma
Giáo viên
27 tháng 11 2023
Lời giải:
a. Để hs trên là hàm bậc nhất thì:
$4m2-4m+1\neq 0$
$\Leftrightarrow (2m-1)^2\neq 0$
$\Leftrightarrow 2m-1\neq 0$
$\Leftrightarrow m\neq \frac{1}{2}$
b.
$f(1)=(4m^2-4m+1).1-3=4m^2-4m-2=6$
$\Leftrightarrow 4m^2-4m-8=0$
$\Leftrightarrow m^2-m-2=0$
$\Leftrightarrow (m+1)(m-2)=0$
$\Leftrightarrow m=-1$ hoặc $m=2$
PT
1
AH
Akai Haruma
Giáo viên
28 tháng 7 2018
Lời giải:
Ta có: \(a+b+c=4m\Rightarrow a+b-c=4m-2c\)
\(\Rightarrow \frac{a+b-c}{2}=2m-c\)
Hoàn toàn tương tự với các phân thức còn lại, suy ra:
\(\left(\frac{a+b-c}{2}\right)^2+\left(\frac{a-b+c}{2}\right)^2+\left(\frac{-a+b+c}{2}\right)^2=(2m-c)^2+(2m-b)^2+(2m-a)^2\)
\(=4m^2+c^2-4mc+4m^2+b^2-4mb+4m^2+a^2-4ma\)
\(=12m^2+a^2+b^2+c^2-4m(a+b+c)\)
\(=12m^2+a^2+b^2+c^2-4m.4m=a^2+b^2+c^2-4m^2\)
Ta có đpcm
CM
13 tháng 6 2018
Đáp án B.
Với x ∈ 5 2 ; 4 thì phương trình tương đương với:
m - 1 log 2 2 x - 2 + m - 5 log 2 x - 2 + m - 1 = 0 (1)
Đặt log 2 ( x - 2 ) = t . Với x ∈ 5 2 ; 4 thì t ∈ - 1 ; 1 . Phương trình (1) trở thành:
( m - 1 ) t 2 + ( m - 5 ) t + m - 1 = 0 ⇔ m ( t 2 + t + 1 ) = t 2 + 5 t + 1 ⇔ m = t 2 + 5 t + 1 t 2 + t + 1 (2)
Xét hàm số f ( t ) = t 2 + 5 t + 1 t 2 + t + 1 = 1 + 4 t t 2 + t + 1 trên đoạn - 1 ; 1 .
Đạo hàm f ' ( t ) = - 4 ( t 2 - 1 ) t 2 + t + 1 ≥ 0 , ∀ t ∈ - 1 ; 1 ; f ' ( t ) = 0 ⇔ t = ± 1 . Khi đó hàm số f ( t ) đồng biến trên - 1 ; 1 . Suy ra min - 1 ; 1 f ( t ) = f ( - 1 ) = - 3 ; max - 1 ; 1 f ( t ) = f ( 1 ) = 7 3 .
Phương trình (2) có nghiệm ⇔ Đường thẳng y - m cắt đồ thị hàm số f ( t ) ⇔ - 3 ≤ m ≤ 7 3 . Vậy S = - 3 ; 7 3 → a = - 3 , b = 7 3 → a + b = - 3 + 7 3 = - 2 3 .
CM
8 tháng 8 2017
Đáp án B.
Với x ∈ 5 2 ; 4 thì phương trình tương đương với:
m - 1 log x 2 x - 2 + m - 5 log 2 x - 2 + m - 1 = 0 (1)
Đặt log 2 x - 2 = t . Với x ∈ 5 2 ; 4 thì t ∈ - 1 ; 1 . Phương trình (1) trở thành:
m - 1 t 2 + m - 5 + m - 1 = 0 ⇔ m t 2 + t + 1 = t 2 + 5 t + 1 ⇔ m = t 2 + 5 t + 1 t 2 + t + 1 (2)
Xét hàm số f ( t ) = t 2 + 5 t + 1 t 2 + t + 1 = 1 + 4 t t 2 + t + 1 trên đoạn - 1 ; 1 .
Đạo hàm f ' ( t ) = - 4 t 2 - 1 t 2 + t + 1 2 ≥ 0 , ∀ t ∈ - 1 ; 1 ; f ' ( t ) = 0 ⇔ t = ± 1 . Khi đó hàm số [-1;1] đồng biến trên [-1;1]. Suy ra m i n [ - 1 ; 1 ] f ( t ) = f ( - 1 ) = - 3 m a x [ - 1 ; 1 ] f ( t ) = f ( 1 ) = 7 3 .
Phương trình (2) có nghiệm ⇔ Đường thẳng y - m cắt đồ thị hàm số
f ( t ) ⇔ - 3 ≤ m ≤ 7 3 . Vậy S = - 3 ; 7 3 → a = - 3 b , b = 7 3 → a = - 3 , b = 7 3 → a + b = - 3 + 7 3 = - 2 3 .