biết tập nghiệm của bất phương trình là x -\(\sqrt{2x+7}\)<= 4 là [a;b]. khi đó 2a+b = ?
giảic chi tiết giúp mình với !!!
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

hoc gioi the hihiihihihhhihihihihiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiii
,mnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnn

TXĐ: \(x>-4\)
Khi đó BPT tương đương:
\(x^2+2x>3\Leftrightarrow x^2+2x-3>0\)
\(\Rightarrow\left[{}\begin{matrix}x>1\\x< -3\end{matrix}\right.\)
Vậy tập nghiệm của BPT là: \(\left[{}\begin{matrix}x>1\\-3< x< -3\end{matrix}\right.\)

Chọn C.
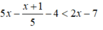
⇔ 25x - (x + 1) - 20 < 10x - 35
⇔ 25x - x - 1 - 20 - 10x + 35 < 0
⇔ 14x + 14 < 0
⇔ x < -1
Vậy tập nghiệm của bất phương trình 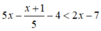 là S = (
-
∞
;-1).
là S = (
-
∞
;-1).

\(\sqrt{x+3}-\sqrt{7-x}>\sqrt{2x-8}\)
⇔ \(\sqrt{x+3}>\sqrt{7-x}+\sqrt{2x-8}\)
⇔ \(\left\{{}\begin{matrix}4\le x\le8\\x+3>7-x+2x-8+2\sqrt{\left(7-x\right)\left(2x-8\right)}\end{matrix}\right.\)
⇔ \(\left\{{}\begin{matrix}4\le x\le8\\x+3>x-1+2\sqrt{\left(7-x\right)\left(2x+8\right)}\end{matrix}\right.\)
⇔ \(\left\{{}\begin{matrix}4\le x\le8\\4>2\sqrt{\left(7-x\right)\left(2x+8\right)}\end{matrix}\right.\)
⇔ \(\left\{{}\begin{matrix}4\le x\le8\\\sqrt{\left(7-x\right)\left(2x-8\right)}< 2\end{matrix}\right.\)
⇔ \(\left\{{}\begin{matrix}4\le x\le8\\-2x^2+22x-56< 2\end{matrix}\right.\)
⇔ \(\left\{{}\begin{matrix}4\le x\le8\\\left[{}\begin{matrix}x>\dfrac{11+\sqrt{5}}{2}\\x< \dfrac{11-\sqrt{5}}{2}\end{matrix}\right.\end{matrix}\right.\)
⇔ \(\left[{}\begin{matrix}4\le x< \dfrac{11-\sqrt{5}}{2}\\\dfrac{11+\sqrt{5}}{2}< x\le8\end{matrix}\right.\)
Các giá trị nguyên của x thỏa mãn là S = {4 ; 7 ; 8}
Ấy chết sai điều kiện XĐ rồi, bạn sửa lại điều kiện thôi nhé

\(a,ĐK:x\ge\dfrac{1}{5}\\ PT\Leftrightarrow5x-1=64\\ \Leftrightarrow x=13\left(tm\right)\\ b,ĐK:x\ge\dfrac{2}{5}\\ BPT\Leftrightarrow5x-2< 16\\ \Leftrightarrow x< \dfrac{18}{5}\\ \Leftrightarrow\dfrac{2}{5}\le x< \dfrac{18}{5}\\ c,ĐK:x\ge3\\ PT\Leftrightarrow\left|x-1\right|-\left|x-2\right|=x-3\\ \Leftrightarrow\left[{}\begin{matrix}1-x-\left(2-x\right)=x-3\left(x< 1\right)\\x-1-\left(2-x\right)=x-3\left(1\le x< 2\right)\\x-1-\left(x-2\right)=x-3\left(x\ge2\right)\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}x=2\left(ktm\right)\\x=0\left(tm\right)\\x=4\left(tm\right)\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=0\\x=4\end{matrix}\right.\)


\(\sqrt{2x-1}< 8-x\)
\(\Leftrightarrow\left\{{}\begin{matrix}2x-1\ge0\\8-x\ge0\\2x-1< \left(8-x\right)^2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x\ge\dfrac{1}{2}\\x\le8\\x^2-18x+65>0\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x\ge\dfrac{1}{2}\\x\le8\\\left[{}\begin{matrix}x>13\\x< 5\end{matrix}\right.\end{matrix}\right.\)
\(\Rightarrow\dfrac{1}{2}\le x< 5\)
Lần sau em đăng trong h nhé!
Hướng dẫn:
\(x-\sqrt{2x+7}\le4\)
<=> \(\sqrt{2x+7}\ge x-4\)(1)
ĐK: x \(\ge\)-7/2
+) Với x - 4 < 0 <=> x < 4 khi đó (1) <=> \(\sqrt{2x+7}\ge0>x-4\) luôn đúng
Đối chiếu đk: x\(\in\)[ -7/2; 4 )
+) Với x - 4 \(\ge\)0 <=> x \(\ge\)4
(1) <=> \(2x+7\ge x^2-8x+16\)
<=> \(x^2-10x+9\le0\)
<=> x\(\in\)[ 1; 9 ]
Đối chiếu đk: x \(\in\)[4; 9 ]
Kết hợp 2 trường hợp ta có: x \(\in\)[ -7/2 ; 9 ]
Vậy a = -7/2; b = 9 nên 2a + b = 2