Thực hiện phép nhân, rút gọn rồi tính giá trị của biểu thức:
a) x(x - y) + y(x + y) tại x = -6 và y = 8;
b) x(x2 - y) - x2 (x + y) + y (x2 – x) tại x = 1212 và y = -100.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
30 tháng 5 2022
a: \(=x^2-xy+xy+y^2=x^2+y^2=100\)
b \(=x^3-xy-x^3-x^2y+x^2y-xy=-2xy=-2\cdot\dfrac{1}{2}\cdot\left(-100\right)=-1\cdot\left(-100\right)=100\)
TC
30 tháng 5 2022
a)` x(x - y) + y(x + y) `
`=x^2-xy+xy+y^2`
`=x^2+y^2`(1)
thay x= -6 ; y= 8 vào 1 ta đc
\(\left(-6\right)^2+8^2=36+64=100\)
b)`) x(x^2 - y) - x^2 (x + y) + y (x^2 - x) `
`=x^3-xy-x^3-xy+yx^2-xy`
`=\(-3xy+yx^2\)(2)
thay `x= 1/2 và y = -100` ta đc
\(-\dfrac{3.1}{2}.\left(-100\right)+\dfrac{\left(-100\right).1}{2}=150-50=100\)
7 tháng 9 2021
a: \(x\left(x-y\right)+y\left(x+y\right)\)
\(=x^2-xy+xy+y^2\)
\(=x^2+y^2\)
=100
b: \(x\left(x^2-y\right)-x^2\left(x+y\right)+y\left(x^2-x\right)\)
\(=x^3-xy-x^3-x^2y+x^2y-xy\)
\(=-2xy\)
CM
21 tháng 4 2018
x(x – y) + y(x + y)
= x.x – x.y + y.x + y.y
= x2 – xy + xy + y2
= x2 + y2.
Tại x = –6 ; y = 8, giá trị biểu thức bằng : (–6)2 + 82 = 36 + 64 = 100.
7 tháng 6 2016
Ta có :
\(x\times\left(x-y\right)+y\times\left(x+y\right)=x^2-xy+xy+y^2=x^2+y^2\)
Thay x= -6 , y= 8 .Ta có:
\(x^2+y^2=\left(-6\right)^2+8^2=36+64=100\)
Vậy \(x\times\left(x-y\right)+y\times\left(x+y\right)=100\)
7 tháng 6 2016
\(x\left(x-y\right)+y\left(x+y\right)\)
=\(x.x-y+y.x+y\)
=\(\left(x.x.x\right)+\left(-y+y+y\right)\)
=\(x^3+y\)
Thay x=-6 và y=8 vào biểu thức \(x^3+y\) ta được
\(x^3+y=\left(-6^3\right)+8=-208\)
Vậy -208 là giá trị của biểu thức \(x^3+y\) tại x=-6 và y=8
19 tháng 2 2020
a) x(x – y) + y (x + y) = x2 – xy +yx + y2= x2+ y2
với x = -6, y = 8 biểu thức có giá trị là (-6)2 + 82 = 36 + 64 = 100
24 tháng 7 2019
x(x - y) + y(x + y)
= x.x + x.(-y) + y.x + y.y
= x2 - xy + xy + y2
= x2 + y2 (1)
Thay x = -6 và y = 8 vào (1), ta có:
x2 + y2 = (-6)2 + 82 = 100
Vậy:...
24 tháng 7 2019
\(A,x\left(x-y\right)+y\left(x+y\right)\)
\(=x^2-xy+xy+y^2\)
\(=x^2+y^2=\left(-6\right)^2+8^2\)
\(=36+64=100\)
25 tháng 7 2016
a) \(x\left(x-y\right)+y\left(x+y\right)=x^2-xy+xy+y^2=x^2+y^2\)
Thay x=-6 ; y=8 ta có:
\(x^2+y^2=\left(-6\right)^2+8^2=36+84=100\)
b)\(x\left(x^2-y\right)-x^2\left(x-y\right)+y\left(x^2-x\right)\\ =x^3-xy-x^3+x^2y+x^2y-xy\\ =2x^2y-2xy\\ =2xy\left(x-1\right)\)
Với x=\(\frac{1}{2}\) ; y=-100 ta có:
\(2xy\left(x-1\right)=2\cdot\frac{1}{2}\cdot\left(-100\right)\cdot\left(\frac{1}{2}-1\right)=-100\cdot-\frac{1}{2}=50\)
và y = –100;
CM
5 tháng 10 2018
x.(x2 – y) – x2.(x + y) + y.(x2 – x)
= x.x2 – x.y – (x2.x + x2.y) + y.x2 – y.x
= x3 – xy – x3 – x2y + x2y – xy
= (x3 – x3) + (x2y – x2y) – xy – xy
= –2xy
Tại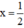 
và y = –100, giá trị biểu thức bằng: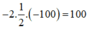 
19 tháng 2 2020
x(x2 – y) – x2 (x + y) + y (x2– x) = x3 – xy – x3 – x2y + yx2 – yx= (2x-2y) – (x2 -2xy +y2) =2(x-y) – (x-y)2
Với x =1/2, y = -100 biểu thức có giá trị là -2 . 1/2. (-100) = 100.
19 tháng 2 2020
x(x2 – y) – x2 (x + y) + y (x2– x) = x3 – xy – x3 – x2y + yx2 – yx= (2x-2y) – (x2 -2xy +y2) =2(x-y) – (x-y)2
Với x =1/2, y = -100 biểu thức có giá trị là -2 . 1/2. (-100) = 100.
a) \(x\left(x-y\right)+y\left(x+y\right)=x^2-xy+xy+y^2=x^2+y^2\) (1)
Thế x = -6 và y = 8 vào (1) ta được:
\(\left(-6\right)^2+8^2=36+64=100\)
b) \(x\left(x^2-y\right)-x^2\left(x+y\right)+y\left(x^2-x\right)\)
\(=x^3-xy-x^3-x^2y+x^2y-xy\)
\(=-2xy\) (2)
Thế x = 1212 và y = -100 vào (2) ta được: \(\left(-2\right).1212.\left(-100\right)=242400\)
a, \(x\left(x-y\right)+y\left(x+y\right)=x^2-xy+xy+y^2=x^2+y^2\left(1\right)\)
Thay \(x=-6,y=8\) vào (1), ta có:
\(x\left(x-y\right)+y\left(x+y\right)=6^2+8^2=36+64=100\)
b, \(x\left(x^2-y\right)-x^2\left(x+y\right)+y\left(x^2-x\right)\)
\(=x^3-xy-x^3-x^2y+x^2y-xy=-2xy\left(2\right)\)
Thay \(x=1212,y=-100\) vào (2), ta được:
\(x\left(x^2-y\right)-x^2\left(x+y\right)+y\left(x^2-x\right)=\left(-2\right).1212.\left(-100\right)=242400\)
Chúc bạn học tốt.