Hình thang ABCD (AB//CD) có AB=4cm;MN=6cm với M và N lần lượt là trung điểm của BC và AD.Khi đó độ dài cạnh CD là...cm
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


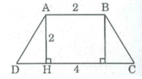
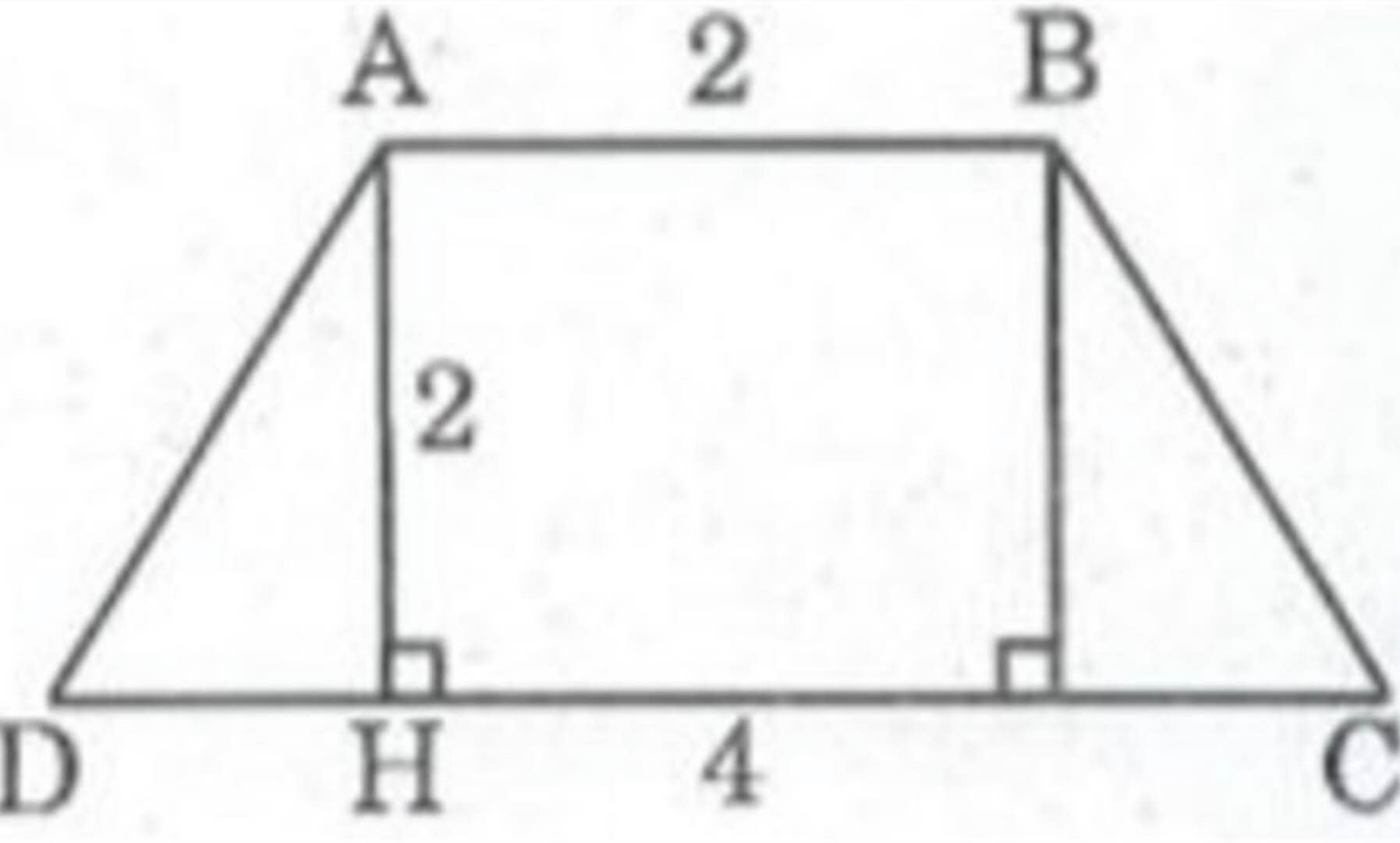
Phân tích: Giả sử hình thang ABCD dựng được thỏa mãn điều kiện bài toán. Tam giác ADH dựng được vì biết hai cạnh góc vuông AH = 2cm và HD = lcm, ∠ H = 90 0 và đáy AB < CD nên ∠ D < 90 0 . Điểm H nằm giữa D và C.
Điểm C nằm trên tia đối tia HD và cách H một đoạn bằng 3 cm
Điểm B thỏa mãn hai điều kiện:
- B nằm trên đường thẳng đi qua A và song song với DH.
- B cách A một khoảng bằng 2cm
Cách dựng:
- Dựng ΔAHD biết ∠ H = 90 0 , AH = 2cm , HD = lcm
- Dựng tia đối của tia HD
- Trên tia đối của tia HD dựng điểm C sao cho HC = 3cm
- Dựng tia Ax // DH, Ax nằm trên nửa mặt phẳng bờ AD chứa điểm H.
- Trên tia Ax, dựng điểm B sao cho AB = 2cm . Nối CB ta có hình thang ABCD cần dựng.
Chứng minh:
Tứ giác ABCD là hình thang vì AB//CD.
Kẻ BK ⊥ CD. Tứ giác ABKH là hình thang có 2 cạnh bên song song nên: BK = AH và KH = AB
Suy ra: KC = HC - KH = HC - AB = 3 - 2 = 1 (cm)
Suy ra: ∆ AHD = ∆ BKC (c.g.c) ⇒ ∠ D = ∠ C
M,N lần lượt là trung điểm của BC và AD nên MN là đường trung bình của hình thang ABCD
=> MN = (AB + CD) : 2 => CD = 2MN - AB = 2.6 - 4 = 8 (cm)