đề bài BM,CM lầ lượt là phận giác của ABC,ACB của ▲aBC;ME vuông góc BA,MF vuông góc AC,MK vuông góc BC
chứng minh ME=MK
chứng minh điểm M nằm trên tia phân giác của BAC
cảm ơn mn ạ!!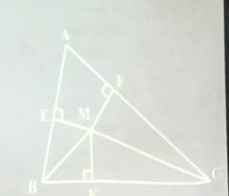
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
30 tháng 7 2023
a: Xét ΔBEM vuông tại E và ΔBKM vuông tại K có
BM chung
góc KBM=góc EBM
=>ΔBEM=ΔBKM
=>ME=MK
b: Xét ΔCKM vuông tại K và ΔCFM vuông tại F có
CM chung
góc KCM=góc FCM
=>ΔCKM=ΔCFM
=>MK=MF=ME
Xét ΔAEM vuông tại E và ΔAFM vuông tại F có
AM chung
ME=MF
=>ΔAEM=ΔAFM
=>góc EAM=góc FAM
=>AM là phân giác của góc BAC
4 tháng 1 2022
a: Xét ΔABM và ΔACN có
\(\widehat{A}\) chung
AB=AC
\(\widehat{ABM}=\widehat{ACN}\)
Do đó: ΔABM=ΔACN
Suy ra: BM=CN và AM=AN
hay ΔAMN cân tại A
b: Xét ΔABC có
AN/AB=AM/AC
Do đó: MN//BC
D
24 tháng 3 2016
a) từ I kẻ IK sao cho KIB=NIB(K thuộc BC)
xét tam giác INB và tam giác IKB có:
NBI=CBI(gt)
IB(chung)
NIB=IKB
suy ra tam giác INB=IKB(g.c.g)
suy ra NIB=BIC
CM tương tự ta có tam giác MIC=KIC(c.g.c)suy ra MIC=KIC
mà NIB=MIC suy ra NIB=BIK=KIC=180/3=60 độ
suy ra BIN=60 độ
29 tháng 1 2024
a: Xét ΔBAC có BM là phân giác
nên \(\dfrac{AM}{AB}=\dfrac{CM}{CB}\)
=>\(\dfrac{AM}{5}=\dfrac{CM}{2}\)
mà AM+CM=AC=5
nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{AM}{5}=\dfrac{CM}{2}=\dfrac{AM+CM}{5+2}=\dfrac{5}{7}\)
=>\(AM=5\cdot\dfrac{5}{7}=\dfrac{25}{7}\left(cm\right);CM=2\cdot\dfrac{5}{7}=\dfrac{10}{7}\left(cm\right)\)
b: Ta có: \(\widehat{ABM}=\widehat{MBC}=\dfrac{\widehat{ABC}}{2}\)
\(\widehat{ACN}=\widehat{NCB}=\dfrac{\widehat{ACB}}{2}\)
mà \(\widehat{ABC}=\widehat{ACB}\)
nên \(\widehat{ABM}=\widehat{MBC}=\widehat{ACN}=\widehat{NCB}\)
Xét ΔABM và ΔACN có
\(\widehat{ABM}=\widehat{ACN}\)
AB=AC
\(\widehat{BAM}\) chung
Do đó: ΔABM=ΔACN
=>AM=AN
Xét ΔABC có \(\dfrac{AM}{AC}=\dfrac{AN}{AB}\)
nên MN//BC
a: Xét ΔBEM vuông tại E và ΔBKM vuông tại K có
BM chung
góc EBM=góc KBM
=>ΔBEM=ΔBKM
=>ME=MK
b: Xét ΔCKM vuông tại K và ΔCFM vuông tại F có
CM chung
góc KCM=góc FCM
=>ΔCKM=ΔCFM
=>MK=MF
=>ME=MF
Xét ΔAEM vuông tại E và ΔAFM vuông tại F có
AM chung
MF=ME
=>ΔAEM=ΔAFM
=>góc EAM=góc FAM
=>AM là phân giác của góc BAC