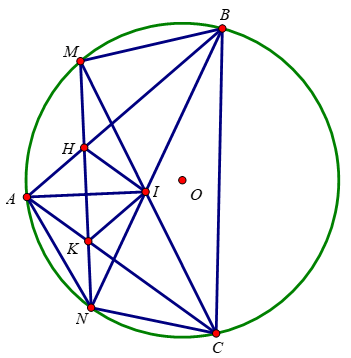
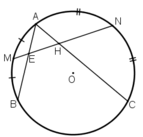
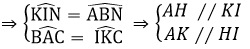cho tam giác ABC nội tiếp đường tròn (O). gọi M là điểm chính giữa cung AB. Vẽ dây MN cắt AC tại K. Chứng minh KM=KC;KN=KA.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


4) Gọi P, Q lần lượt là tâm của các đường tròn ngoại tiếp tam giác MBK, tam giác MCK và E là trung điểm của đoạn PQ. Vẽ đường kính ND của đường tròn (O) . Chứng minh ba điểm D, E, K thẳng hàng.

Vì N là điểm chính giữa cung nhỏ BC nên DN là trung trực của BC nên DN là phân giác B D C ^
Ta có K Q C ^ = 2 K M C ^ (góc nọi tiếp bằng nửa góc ở tâm trong dường tròn (Q))
N D C ^ = K M C ^ (góc nội tiếp cùng chắn cung N C ⏜ )
Mà B D C ^ = 2 N D C ^ ⇒ K Q C ^ = B D C ^
Xét 2 tam giác BDC & KQC là các các tam giác vuông tại D và Q có hai góc ở ⇒ B C D ^ = B C Q ^ do vậy D, Q, C thẳng hàng nên KQ//PK
Chứng minh tương tự ta có ta có D, P, B thẳng hàng và DQ//PK
Do đó tứ giác PDQK là hình bình hành nên E là trung điểm của PQ cũng là trung điểm của DK. Vậy D, E, K thẳng hàng (điều phải chứng minh).

1: M là điểm chính giữa của cung AC
=>MA=MC
mà OA=OC
nên OM là trung trực của AC
=>OM vuông góc AC tại K
góc AHO+góc AKO=180 độ
=>AHOK nội tiếp
3: Gọi G là trung điểm của AB
ΔOAB cân tại O
mà OG là trung tuyến
nên OG là trung trực của AB
=>OH là một phần đường kính của đường tròn ngoại tiếp ΔOAB
Xet ΔABC co BH/BA=BO/BC
nên OH//AC
=>OH vuông góc OM
=>OM tiếp xúc với đường tròn ngoại tiêp ΔABC

+ Do góc  là góc có đỉnh bên trong đường tròn chắn hai cung
là góc có đỉnh bên trong đường tròn chắn hai cung 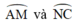
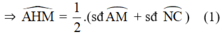
+ Do góc  là góc có đỉnh bên trong đường tròn chắn hai cung
là góc có đỉnh bên trong đường tròn chắn hai cung 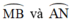
+ Do M và N là điểm chính giữa của cung A B ⏜ v à A C ⏜
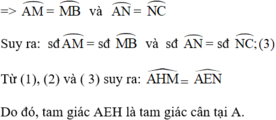

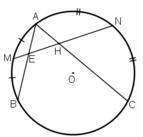
+ Do góc  là góc có đỉnh bên trong đường tròn chắn hai cung
là góc có đỉnh bên trong đường tròn chắn hai cung ![]()
![]()
+ Do góc  là góc có đỉnh bên trong đường tròn chắn hai cung
là góc có đỉnh bên trong đường tròn chắn hai cung 

Kiến thức áp dụng
+ Số đo của góc có đỉnh ở bên trong đường tròn bằng nửa tổng số đo hai cung bị chắn.

a) Xét tứ giác HMBI có:
∠HMI = ∠HBI (2 góc nội tiếp chắn 2 cung bằng nhau \(\widebat{AN}=\widebat{CN}\))
Mà 2 góc này cùng nhìn cạnh HI
=> Tứ giác BMHI nội tiếp
b) Xét ΔMNI và ΔMKC có:
∠KMC là góc chung
∠MNI = ∠KCM (2 góc nội tiếp chắn 2 cung bằng nhau \(\widebat{AM}=\widebat{BM}\))
=> ΔMNI ∼ ΔMCK => \(\frac{MN}{MC}=\frac{MI}{MK}\) => MN.MK = MC.MI
c) Xét tứ giác NKIC có:
∠KNI = ∠KCI (2 góc nội tiếp chắn 2 cung bằng nhau \(\widebat{AM}=\widebat{MB}\))
Mà 2 góc này cùng nhìn cạnh KI
=> Tứ giác NKIC là tứ giác nội tiếp
=> ∠NKI + ∠NCI = 180o (1)
Xét đường tròn (O) có:
\(\hept{\begin{cases}\widehat{ANK}=\widehat{ACM}\left(\text{2 góc nội tiếp cùng chắn cung AM}\right)\\\widehat{NAK}=\widehat{NCA}\left(\text{2 góc nội tiếp cùng chắn 2 cung BẰNG NHAU}\widebat{AN}=\widebat{CN}\right)\end{cases}}\)
=> ∠ANK + ∠NAK = ∠ACM + ∠NCA = ∠NCI (2)
Xét tam giác AKN có: ∠ANK + ∠NAK + ∠NKA = 180o (3)
Từ (1), (2), (3) => ∠NKI = ∠NKA
Xét tam giác IKN và tam giác AKN có:
∠NKI = ∠NKA
KN là cạnh chung
∠KNI = ∠KNA (2 góc nội tiếp chắn 2 cung bằng nhau)
=> ΔIKN = ΔAKN
=> IK=AK =>ΔAKI cân tại K
Tứ giác NKIC là tứ giác nội tiếp
Mặt khác ∠KCN = ∠ABN (2 góc nội tiếp cùng chắn cung AN của (O))
∠BAC = ∠BNC (2 góc nội tiếp cùng chắc cung BC của (O))
=> Tứ giác AHIK là hình bình hành
Mà IK = AK
=> Tứ giác AHIK là hình thoi.
CÒN LẠI TỰ LÀM LÀM NHA

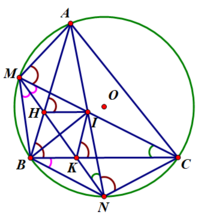
2) Chứng minh N B 2 = N K . N M .
Ta có N là điểm chính giữa cung B C ⏜ ⇒ B N ⏜ = C N ⏜ ⇒ B M N ^ = C M N ^ (góc nội tiếp chắn 2 cung bằng nhau)
Mà C B N ^ = C M N ^ (góc nội tiếp chắn cùng chắn cung C N ⏜ )
C B N ^ = B M N ^ (cùng bằng góc C M N ^ ) ⇒ K B N ^ = B M N ^
Xét Δ K B N v à Δ B M N có:
N ^ chung
K B N ^ = B M N ^
⇒ Δ K B N ∽ Δ B M N ⇒ K N B N = B N M N ⇒ N B 2 = N K . N M
(điều phải chứng minh).

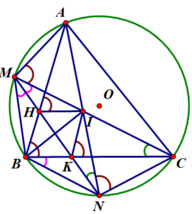
3) Chứng minh tứ giác BHIK là hình thoi.
Ta có A B C ^ = A N C ^ (góc nội tiếp cùng chắn cung A C ⏜ )
Mà A M C ^ = A H I ^ (góc nội tiếp cùng chắn cung I C ⏜ )
⇒ A B C ^ = I K C ^ Mà 2 góc này ở vị trí đồng vị nên H B / / I K (1)
+ Chứng minh tương tự phần 1 ta có tứ giác AMHI nội tiếp
A N C ^ = I K C ^ (góc nội tiếp cùng chắn cung A I ⏜ )
Ta có A B C ^ = A M C ^ (góc nội tiếp cùng chắn cung A C ⏜ )
⇒ A B C ^ = A H I ^ Mà 2 góc này ở vị trí đồng vị nên B K / / H I (2)
Từ (1) và (2) suy ra tứ giác BHIK là hình bình hành.
Mặt khác AN, CM lần lượt là các tia phân giác của các góc A và C trong tam giác ABC nên I là giao điêm 3 đường phân giác, do đó BI là tia phân giác góc B
Vậy tứ giác BHIK là hình thoi (dấu hiệu nhận biết hình thoi).