Cho tam giác ABC, M là trung điểm của BC. Trên tia đối của của tia MA lấy điểm E sao cho ME
= MA. Chứng minh rằng:
a) AC = EB và AC // BE
b)Gọi I là một điểm trên AC;K là một điểm trên EB sao cho AI=EK . Chứng minh bađiểm I , M , K thẳng hàng
c) Từ E kẻ EH BC H BC Biết HBE= 50o;MEB=25o.Tính HEMvàBME
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Hơi khó nhìn,nếu bạn không hiểu phần nào bạn hỏi mình nhé.Nếu bạn có ý kiến gì về bài giải và phương pháp giải của mình bạn có thể hỏi mình nha.Mình sẽ trả lời bạn.


a: Xét tứ giác ACEB có
M là trung điểm của BC
M là trung điểm của AE
Do đó: ACEB là hình bình hành
Suy ra: AC//BE

Bài 1:
a: Xét ΔMAC và ΔMEB có
MA=ME
\(\widehat{AMC}=\widehat{EMB}\)(hai góc đối đỉnh)
MC=MB
Do đó: ΔMAC=ΔMEB
=>AC=EB
Ta có: ΔMAC=ΔMEB
=>\(\widehat{MAC}=\widehat{MEB}\)
mà hai góc này là hai góc ở vị trí so le trong
nên AC//BE
b: Xét ΔIAM và ΔKEM có
IA=KE
\(\widehat{IAM}=\widehat{KEM}\)
AM=EM
Do đó: ΔIAM=ΔKEM
=>\(\widehat{IMA}=\widehat{KME}\)
=>\(\widehat{IMA}+\widehat{AMK}=180^0\)
=>I,M,K thẳng hàng
Bài 2:
2xy-x-y=12
=>x(2y-1)-y+1/2=12,5
=>\(2x\left(y-\dfrac{1}{2}\right)-\left(y-\dfrac{1}{2}\right)=12,5\)
=>\(2x\left(2y-1\right)-\left(2y-1\right)=25\)
=>\(\left(2x-1\right)\left(2y-1\right)=25\)
=>\(\left(2x-1;2y-1\right)\in\left\{\left(1;25\right);\left(25;1\right);\left(-1;-25\right);\left(-25;-1\right);\left(5;5\right);\left(-5;-5\right)\right\}\)
=>\(\left(x,y\right)\in\left\{\left(2;13\right);\left(13;2\right);\left(0;-12\right);\left(-12;0\right);\left(3;3\right);\left(-2;-2\right)\right\}\)

GIAI
a/Xet tam giac ACM va tam giac BME,co :
AM=MẸ̣̣̣(gt)
BM=MC̣̣̣̣̣̣̣(gt)
gocAMC=gocBME(ḍḍ)
Vay tam giac AMC = tam giac EMB(cgc)
Suy ra goc MAC = goc MEB(2 goc tuong ung)
ma goc MAC va goc MBE la 2 goc so le trong
nen AC//BE
b/Taco goc BMI+IMC=180
ma goc IMC= goc BMK(dd)
nen goc BMI+ gocBMK=180
Vay 3 diem I,M,K thang hang
TA có;AM=EM và BM=CM
Suy ra;AE và BC cắt nhau tại trung điểm M (câu a)
Do đó;tứ giác ABEC là hình binh hành
Nên AC song song với BE
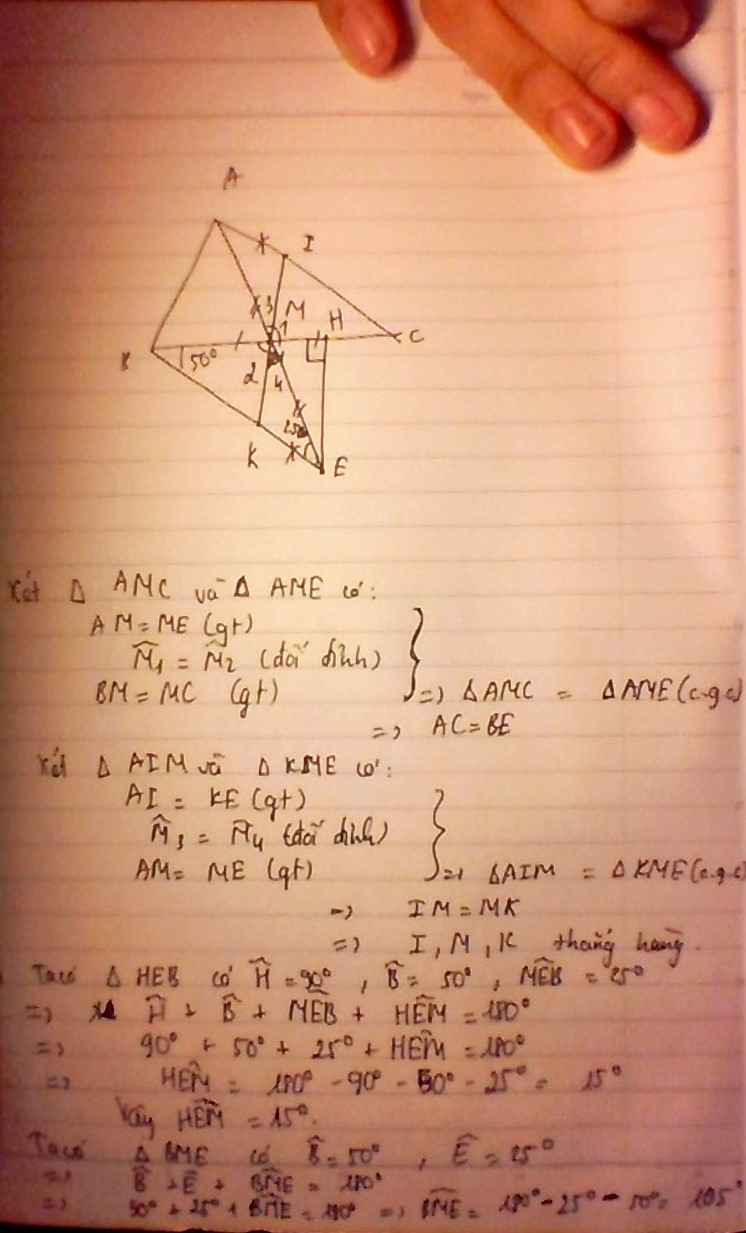


a) xét
\(\Delta BME\text{VÀ}\Delta CMA\\ BM=CM\left(gt\right)\\ \widehat{BME}=\widehat{CMA}\\ MA=ME\left(gt\right)\\ \Delta BME=\Delta CMA\left(c-g-c\right)\Rightarrow BE=AC\\ \widehat{EMB}=\widehat{ACM}\left(\text{MÀ Ở VỊ TRÍ SO LE TRONG}\right)\\ \Rightarrow AC\text{//}BE\)
:V lười gõ tiếp quá ;-;
mà bạn cho mình hỏi. =) mình thấy bạn đăng toàn câu hỏi nâng cao bạn đang thi HSG hả ;-; mình 24/1 thi rồi =) không biết bạn có thi không =)))
a, xét tam giác MAC và tâm giác MEB
có{ME=MA(gt);BM=MC;tam giác MAC= tam giác MEB(c-g-c)
=> AC = EB=>EMB^=ACM^( mà ở vị trí so le trong)
=> AC// BE
b, Xét tam giác AIM và tam giác KME
có { AI=KE(gt);M3^=M4^; AM=ME(gt)
=> tam giác AIM= tam giác KME(c-g-c)
=> IM=MK
=> I,M,K thẳng hàng
c, ta có : tam giác HEB
có { H^ =90°;B^ =50°;MEB^=25°
=> H^ + B^ + MEB^ +HEM^ =180°
=> 90°+50°+25°+HEM^ =180°
=> HEM^ =180°-90°-50°-25°
=> HEM^=15°
lại có tam giác BME
{B^=50°;E^=25°
=> B^+E^+BME^= 180°
=> BME^ = 180° -25°-50°
=> BME^ =105°