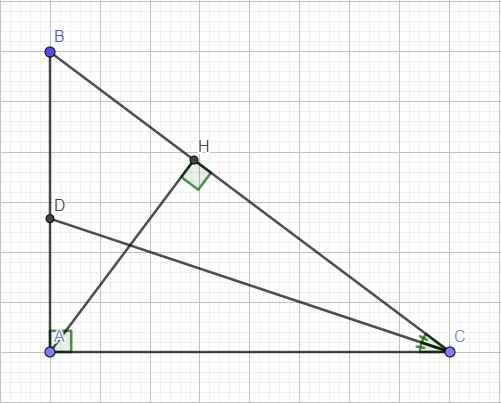
Cho tam giác ABC vuong tại A có AB=3cm,AC=4cm.kẻ đg cao AH(H thuộc BC)
a)Tính độ dài BC
b)So sánh HB&HC
c)Trên tia đối HA lấy điểm D sao cho HD=HA.Chứng mih tam giác ACD cân
d)kẻ DK vuông góc vs AC(K thuộc AC).chứng mih AI vuông góc VS DC và AI // BD
GIẢI HỘ MH VS ĐANG GẤP LẮM:))



a) Áp dụng định lí Pi-ta-go vào tam giác ABC vuông tại A có:
AB2 + AC2 = BC2
=> 32 + 42 = BC2
=> BC2 = 25
=> BC= 5 cm
b) Áp dụng định lí Pi-ta-go vào tam giác AHB vuông tại H có:
HB2 + HA2 = AB2
=> HB2 = AB2 - HA2
=> HB2 = 9 - HA2 (1)
Áp dụng định lí Pi-ta-go vào tam giác AHC vuông tại H có:
HC2 + HA2 = AC2
=> HC2 = AC2 - HA2
=> HC2\(\sqrt{HC}\) = 16 - HA2 (2)
Từ (1) và (2) => HC2 > HB2 => HC > HB
c) Xét tam giác ACD có:
AH là đường cao của tam giác ACD ( AH vuông góc BC )
AH là đường trung tuyến của tam giác ACD ( HB = HA)
=> tam giác ACD cân tại A (tam giác có 2 trong 4 đường: trung trực, trung tuyến, phân giác, đường cao trùng nhau là tam giác cân)
CHO MK HỎI ĐIỂM I Ở ĐÂU VẬY! TỰ NHIÊN CÂU D CÓ ĐIỂM I