Cho tam giác ABC nhọn đường cao AH. Gọi M là trung điểm của AC; D là điểm đối xứng với B qua M. Trên tia đối của tia AD lấy điểm E sao cho AD = He. Chứng minh HE = CD
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Lời giải:
Điểm H trong bài không đóng vai trò gì thì không nên đưa vào bài.
Vì $B,D$ đối xứng nhau qua $M$ nên $M$ là trung điểm $BD$
Tứ giác $ABCD$ có 2 đường chéo $AC, BD$ cắt nhau tại trung điểm $M$ của mỗi đường nên $ABCD$ là hình bình hành.

Xét ΔAHC có
I là trung điểm của AH
N là trung điểm của AC
DO đó: IN là đường trung bình của ΔAHC
Suy ra: \(IH=3cm\)


Bạn tự vẽ hình giúp mình nhé!
Xét tam giác AHC vuông tại H có:
HM là đường trung tuyến ứng với cạnh huyền AC
\(\Rightarrow HM=AM=MC=MN\)
\(\Rightarrow HN=AC\) (1)
Xét tam giác HMC và tam giác NMA có:
\(\left\{{}\begin{matrix}AM=MC\\\widehat{AMN}=\widehat{CMH}\left(đđ\right)\\HM=MN\end{matrix}\right.\)
\(\Rightarrow\Delta HMC=\Delta NMA\)
\(\Rightarrow\widehat{MHC}=\widehat{MNA}\)
Mà hai góc trên nằm ở vị trí so le
\(\Rightarrow\)AN//HC(2)
Chứng minh tương tự ta được AH//NC(3)
Từ (1),(2),(3) suy ra, tứ giác AHCN là hình chữ nhật

Lời giải:
$M,N$ lần lượt là trung điểm $AB, AC$ nên $MN$ là đường trung bình của tam giác $ABC$ ứng với cạnh $BC$
$\Rightarrow MN\parallel BC$ hay $MN\parallel HP$
$\Rightarrow MNPH$ là hình thang $(*)$
Mặt khác:
Tam giác vuông $ABH$ có $HM$ là đường trung tuyến ứng với cạnh huyền nên $HM=\frac{AB}{2}=MB$ (bổ đề quen thuộc)
$\Rightarrow $MHB$ cân tại $M$
$\Rightarrow \widehat{MHB}=\widehat{MBH}$
Mà $\widehat{MBH}=\widehat{NPC}$ (hai góc đồng vị với $NP\parallel AB$)
$\Rightarrow \widehat{MHB}=\widehat{NPC}$
$\Rightarrow 180^0-\widehat{MHB}=180^0-\widehat{NPC}$
Hay $\widehat{MHP}=\widehat{NPH}(**)$
Từ $(*); (**)\Rightarrow $MNPH$ là hình thang cân (đpcm)

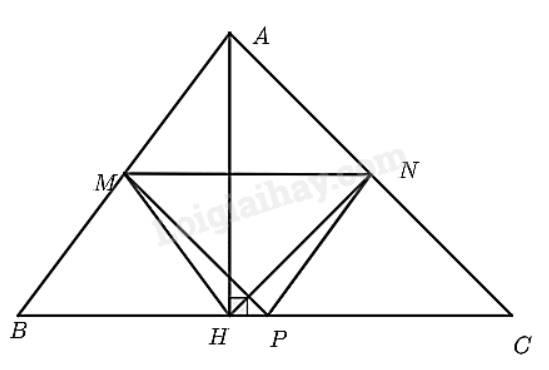
- Vì \(M\) là trung điểm của \(AB;N\) là trung điểm của \(AC\) nên \(MN\) là đường trung bình của tam giác \(ABC\). Do đó, \(MN//BC\) (tính chất đường trung bình).
\( \Rightarrow MN//HP\left( {H;P \in BC} \right)\)
Xét tứ giác \(MNPH\) có: \(MN//HP \Rightarrow \) tứ giác \(MNPH\) là hình thang.
- Vì \(M\) là trung điểm của \(AB;P\) là trung điểm của \(AC\) nên \(MP\) là đường trung bình của tam giác \(ABC\). Do đó, \(MP = \frac{1}{2}AC\) (tính chất đường trung bình) (1).
- Xét tam giác \(AHC\) vuông tại \(H\) có:
\(N\)là trung điểm của \(AC\) nên \(HN = \frac{1}{2}AC\) (tính chất đường trung tuyến ứng với cạnh huyền trong tam giác vuông) (2).
Từ (1) và (2) suy ra \(MP = HN\).
Xét hình thang \(MNPH\) có: \(MP = HN\) (chứng minh trên).
Do đó, hình thang \(MNPH\) là hình thang cân (dấu hiệu nhận biết hình thang cân).
Đề sai rồi bạn