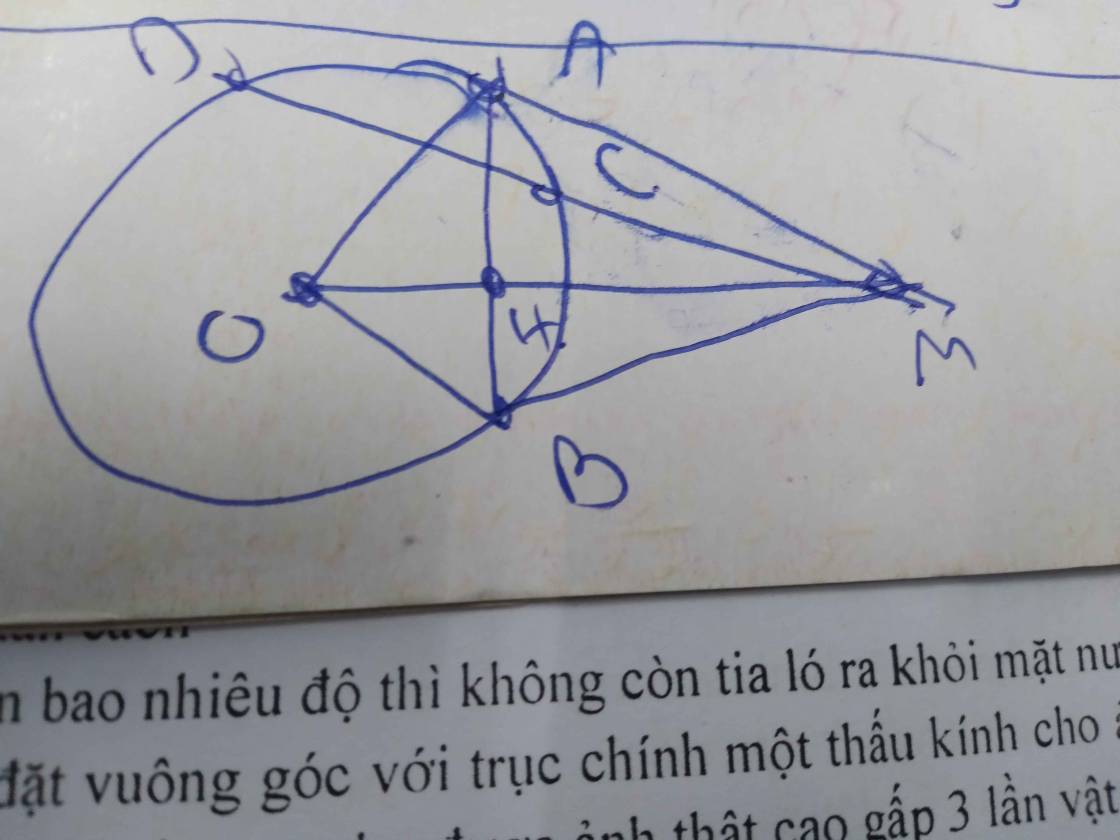
Từ M bên ngoài (0) vẽ cát tuyến MCD và 2 tiếp tuyến MA,MB ( A,B là các tiếp điểm). C nằm giữa M;D.
C/m a) MA^2=MC.MD
b) Gọi I là trung điểm CD. C/m M,A,O,I,B cùng nằm trên 1 đường tròn
c) H là giao điểm của AB và MO. C/m CHOD nội tiếp. từ đó suy ra AB là đường phân giác góc CHD
d) Gọi K là giao điểm tiếp tuyến tại C,D của (0). C/m A,B,K thẳng hàng