Cho ∆ABC cân tại A. Kẻ BH ⊥ AC; CK ⊥ AB.
a, Chứng minh : ∆ABH = ∆ACK
b, Chứng minh : ∆AHK cân
c, Gọi I là giao điểm của BH và CK; AI cắt BC tại M. Chứng minh: IM là phân giác của \(\widehat{BIC}\)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét ΔAHB vuông tại H và ΔAKC vuông tại K có
AB=AC
\(\widehat{BAH}\) chung
Do đó: ΔAHB=ΔAKC
b: Xét ΔAKD vuông tại K và ΔAHD vuông tại H có
AD chung
AK=AH
Do đó: ΔAKD=ΔAHD

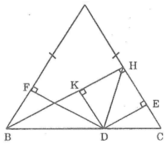
Kẻ DK ⊥ BH
Ta có: BH ⊥AC(gt)
Suy ra: DK // AC (hai đường thẳng cùng vuông góc với đường thẳng thứ ba thì song song)
⇒ ∠KDB = ∠C (hai góc đồng vị)
VìΔABC cân tại A nên ∠B = ∠C (tính chất tam giác cân)
Suy ra: ∠KDB = ∠B
Xét hai tam giác vuông BFD và DKB, ta có:
∠BFD = ∠DKB = 90o
BD cạnh huyền chung
∠FBD = ∠KDB (chứng minh trên)
Suy ra:ΔBFD=ΔDKB (cạnh huyền góc nhọn)
⇒ DF = BK (hai cạnh tương ứng)(1)
Nối DH. Xét ΔDEH và ΔHKD, ta có:
∠DEH = ∠DKH = 90o
DH cạnh huyền chung
∠EHD = ∠KDH (hai góc so le trong)
Suy ra:ΔDEH = ΔDKH( cạnh huyền , góc nhọn)
Suy ra: DE = HK ( hai cạnh tương ứng) (2)
Mặt khác: BH = BK + KH (3)
Từ (1), (2) và (3) suy ra: DF + DE = BH

bài 1 ta có :
AC=AH+HC=6+4=10cm
Vì ΔABC cân tại A nên AB=AC=10cm
Vì ΔABH vuông tại H
⇒AB\(^2\)=AH\(^2\)+BH\(^2\)
⇒10\(^2\)=6\(^2\)+BH\(^2\)
⇒BH=8cm
Vì ΔBHC vuông tại H
⇒BC\(^2\)=BH\(^2\)+CH\(^2\)
⇒BC\(^2\)=8\(^2\)+4\(^2\)
⇒BC=4\(\sqrt{5}\)cm

a) Xét ΔABH vuông tại H và ΔACH vuông tại H có
AB=AC(ΔABC cân tại A)
AH chung
Do đó: ΔABH=ΔACH(cạnh huyền-cạnh góc vuông)
Suy ra: BH=CH(hai cạnh tương ứng)
b) Xét ΔEHB vuông tại E và ΔFHC vuông tại F có
HB=HC(cmt)
\(\widehat{B}=\widehat{C}\)(hai góc ở đáy của ΔABC cân tại A)
Do đó: ΔEHB=ΔFHC(cạnh huyền-góc nhọn)
Suy ra: HE=HF(hai cạnh tương ứng)
Xét ΔHEF có HE=HF(cmt)
nên ΔHEF cân tại H(Định nghĩa tam giác cân)

A B C H 7 cm 2 cm 2 cm
Ta có: AC = AH + HC = 7 + 2 = 9 (cm)
Vì AB = AC => AB = 9 cm
Áp dụng định lí Pi - ta - go vào t/giác AHB vuông tại H, ta có:
AB2 = AH2 + BH2
=> BH2 = AB2 - AH2 = 92 - 72 = 32
Áp dụng định lí Pi - ta - go vào t/giác AHC vuông tại H, ta có:
BC2 = BH2 + HC2 = 32 + 22 = 36
=> BC = 6 (cm)

Do \(\Delta ABC\) cân tại A \(\Rightarrow\widehat{BCA}=\widehat{CBA}\) hay \(\widehat{BCH}=\widehat{CBA}\)
Xét hai tam giác vuông BHC và CKB có:
\(\left\{{}\begin{matrix}BC\text{ chung}\\\widehat{BCH}=\widehat{CBK}\end{matrix}\right.\) \(\Rightarrow\Delta_VBHC=\Delta_VCKB\left(ch-gn\right)\)
\(\Rightarrow CH=BK\) (1)
Mà \(\Delta ABC\) cân tại A \(\Rightarrow AB=AC\)
\(\Rightarrow AK+BK=AH+CH\) (2)
(1);(2) \(\Rightarrow AK=AH\)
\(\Rightarrow\Delta AHK\) cân tại A

a: Xet ΔAHB vuông tại H và ΔAKC vuông tại K có
AB=AC
góc BAH chung
=>ΔAHB=ΔAKC
b: ΔHBA=ΔKAC
=>AH=AK
=>ΔAHK cân tại A
c: góc KBC+góc ICB=90 độ
góc HCB+góc IBC=90 độ
mà góc KBC=góc HCB
nên góc IBC=góc ICB
=>ΔIBC cân tại I
mà IM là đường cao
nên IM là phân giác của góc BIC