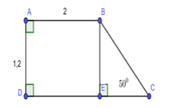
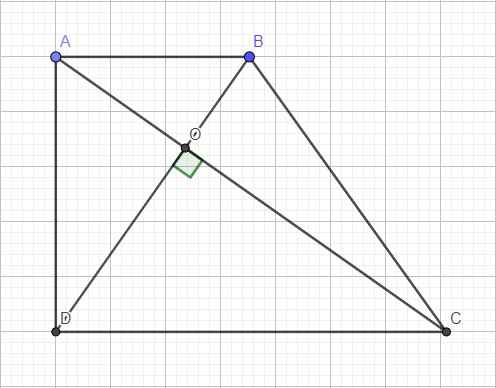
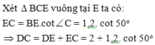cho hình thang ABCD vuông tại A và D. biết AB=a;CD=b;BC=a+b.O là trung điểm của AD.trên BC lấy E sao cho BE=a
a) chứng minh: AD^2 =4ab
b) Gọi I là giao điểm của OC với DE,H là giao điểm của OB với AE. Tứ giác OIEH ; AHID là hình gì?
c) tính diện tích tứ giác OIEH và AHID
mình đang cần gấp. Ai giải đc mk sẽ tích 5 lần cho người ấy! .....^-^