Cho hbh ABCD có góc A<90 độ. Đường tròn (A;AB) cắt đường thẳng BC tại E. (C;CB) cắt đường thẳng AB tại K. c/m
a) DE=DK
b) A,D,C,K,E cùng thuộc 1 đường tròn
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

bn tham khảo tại đây nhé :
Bài 57 Sách bài tập - tập 2 - trang 98 - Toán lớp 8 | Học trực tuyến
tuy ko giống hết nhưng bn có thể dựa vào đó mà tham khảo

Lời giải:
Vì $ABCD$ là hình bình hành nên $AB\parallel CD$
$\Rightarrow AE\parallel CF(1)$
Vì $ABCD$ là hình bình hành nên $AB=CD$
$\Rightarrow \frac{1}{2}AB=\frac{1}{2}CD$
$\Rightarrow AE=CF(2)$
Từ $(1); (2)$ xét tứ giác $AECF$ có 2 cạnh đối $AE, CF$ song song và bằng nhau nên $AECF$ là hình bình hành.

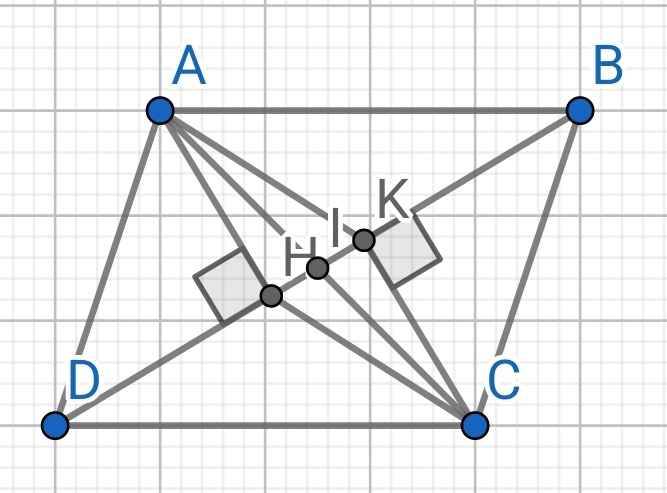 a) Do ABCD là hình bình hành (gt)
a) Do ABCD là hình bình hành (gt)
⇒ AD // BC
⇒ ∠ADH = ∠CBK (so le trong)
Do AH ⊥ BD (gt)
CK ⊥ BD (gt)
⇒ AH // CK
∆AHD và ∆CKB có:
AD = BC (hai cạnh đối của hình bình hành)
∠ADH = ∠CBK (cmt)
⇒ ∆AHD = ∆CKB (cạnh huyền - góc nhọn)
⇒ AH = CK (hai cạnh tương ứng)
Tứ giác AHCK có:
AH // CK (cmt)
AH = CK (hai cạnh tương ứng)
⇒ AHCK là hình bình hành
b) Do AHCK là hình bình hành (cmt)
I là trung điểm HK (gt)
⇒ I là trung điểm AC
Do ABCD là hình bình hành (gt)
I là trung điểm AC (cmt)
⇒ I là trung điểm BD
⇒ IB = ID

Đề bài sai vì:
AC=CD là đương nhiên vì là hai cạnh đối nhau của hbh (t/c hbh)
=> Dữ kiện đúng phải là AB=BC hoặc AB=AD

a) Xét hai tam giác vuông HAD và KCB có :
AD = BC ( vì ABCD là hình bình hành )
góc A1 = góc C1 ( so le trong ; AD // BC )
Suy ra t/g HAD = t/g KCB ( ch-gn )
Suy ra DH = BK
DH // BK ( vì DH vuông góc AC , BK vuông góc AC )
Suy ra DHBK là hình bình hành
b) ABCD là hình bình hành ( gt )
mà O là trung điểm của AC ( gt )
Suy ra O là trung điểm BD
Mà DHBK là hình bình hành ( cmt )
Suy ra O là trung điểm HK
1Tam giác ABK bằng tam giác CHD theo Trường hợp canh huyền góc nhìn
Suy ra BK bằng DH mà BK song song DH cùng vuông góc với AC nên suy ra tứ giác BKDH là hình bình hành
2 hcn ABCD có hai đường cho cắt nha tại trung điểm mỗi đường mà O là trung điểm của AC nên suy ra O là trung điểm của BD
HbhBKDH có hai đường cho cắt nhau tại trung điểm của mỗi đường mà O là trung điểm của BD suy ra O là trung điểm của KH
a.
Từ giả thiết \(\Rightarrow AE=AB\) (cùng là bán kính của (A;AB))
Mà \(AB=DC\Rightarrow AE=DC\)
Hoàn toàn tương tự, ta có \(CK=BC=AD\)
\(\Delta ABE\) cân tại A, \(\Delta CBK\) cân tại C \(\Rightarrow\left\{{}\begin{matrix}\widehat{ABE}=\widehat{AEB}\\\widehat{CBK}=\widehat{CKB}\end{matrix}\right.\)
Mà \(\widehat{ABE}=\widehat{CBK}\) (đối đỉnh)
\(\Rightarrow\widehat{EAB}=\widehat{KCB}\)
Lại có \(\widehat{BAD}=\widehat{BCD}\) (hai góc đối hbh)
\(\Rightarrow\widehat{EAD}=\widehat{DCK}\)
Xét hai tam giác EAD và DCK có: \(\left\{{}\begin{matrix}AE=DC\left(cmt\right)\\\widehat{EAD}=\widehat{DCK}\left(cmt\right)\\AD=CK\left(cmt\right)\end{matrix}\right.\)
\(\Rightarrow\Delta EAD=\Delta DCK\left(c.g.c\right)\Rightarrow DE=DK\)
b.
Do \(\left\{{}\begin{matrix}AB||CD\\AD=CK\end{matrix}\right.\) \(\Rightarrow ADCK\) là hình thang cân
\(\Rightarrow\) ADCK nội tiếp (1)
Đồng thời ta có \(\widehat{ACD}=\widehat{KDC}\)
Mà \(\Delta EAD=\Delta DCK\left(cmt\right)\Rightarrow\widehat{KDC}=\widehat{DEA}\)
\(\Rightarrow\widehat{ACD}=\widehat{DEA}\)
\(\Rightarrow AECD\) nội tiếp (2 góc bằng nhau cùng chắn cung AD) (2)
(1);(2) \(\Rightarrow A,D,C,K,E\) cùng thuộc 1 đường tròn